在本节课中,我们首先讲述4个关于网络的重要属性,它们是我们研究图的重要指标。然后介绍几种常见的随机图模型。
Measuring Networks via Network Properties
在本节中,我们将研究四个关键网络属性以表征图形:
- 度分布——$P(k)$
- 路径长度——$h$
- 聚类系数——$C$
- 连接组件——$s$
这些定义主要是针对无向图的,但可以轻松地将其扩展为有向图。
Degree Distribution

度分布 $P(k)$ 表示随机选择一个节点,它具有度 $k$ 的概率是多少。对于一个已知的图 $G$ ,它的度分布可以通过归一化的直方图来概括,其中我们通过节点总数来归一化直方图。
我们可以通过 $P(k)=N_{k}/N$ 计算图的度分布。其中,$N_{k}$ 是度为 $k$ 的节点数,$N$ 为节点总数。可以将度分布视为随机选择的节点具有度 $k$ 的概率。
如果要将这些定义扩展为有向图,需要分别计算入度和出度的分布。
Paths in a Graph
path
路径是一系列节点,其中每个节点都链接到下一个节点:
$$
P_{n} = \lbrace {i_{0},i_{1},i_{2},…,i_{n}} \rbrace
$$
其中 $\lbrace{(i_{0},i_{1}),(i_{1},i_{2}),(i_{2},i_{3}),…(i_{n-1},i_{n})\rbrace} \in E$
distance
一对节点之间的距离(也称最短路径,geodesic)定义为沿着连接这对节点的最短路径的边数。
如果两个节点未连接,则距离通常定义为无限(或零)。 人们还可以将距离视为遍历从一个节点到另一个节点所需的最少节点数。
在有向图中,路径需要遵循箭头的方向。 因此,有向图的距离不是对称的。 对于具有加权边的图,距离是从一个节点到另一个节点所需要遍历的最小边权重。
Average path length
图的平均路径长度(Average path length)是所有连接的节点之间中最短路径的平均值。 我们将计算平均路径长度定义为 $$ \hat{h}=\frac{1}{2 E_{max }} \sum_{i, j \neq i} h_{i j} $$ 其中 $E_{max}$ 是边或节点对的最大数目;也就是说 $E_{max}=n(n-1)/2$ 和 $h_{ij}$ 是从 $i$ 节点到 $j$ 节点的距离。注意,我们仅计算连接的节点对上的平均路径长度,因此忽略了无限长度的路径。
Clustering Coefficient
聚类系数(针对无向图)用于衡量节点 $i$ 的邻居相互联系的程度。
对于度数为 $k_{i}$的节点 $i$,我们计算聚类系数为 $$ C_{i}=\frac{2e_{i}}{k_{i}(k_{i}-1)} $$ 其中 $e_{i}$ 是节点 $i$ 的相邻节点之间的边数。 注意 $C_{i}\in[0,1]$ 。
此外,对于度数为0或1的节点,聚类系数是不确定的。
同样,可以计算平均聚类系数为: $$ C=\frac{1}{N}\sum_{i}^{N}C_{i} $$ 平均聚类系数使我们能够看到边在网络的某些部分是否显得更加密集。
在社交网络中,平均聚类系数趋于很高,表明如我们期望的那样,朋友的朋友倾向于彼此认识。
Connectivity/Connected Components
图的连通性指的是图中最大连通组件的大小。
最大的连通组件是可以通过路径将任意两个顶点连接在一起的图的最大的集合。
寻找连接的组件:
- 从随机节点开始并执行广度优先搜索(BFS)
- 标记BFS访问的节点
- 如果访问了所有节点,则表明网络是连通的
- 否则,找到一个未访问的节点并重复BFS
A real-world network example——MSN Messenger
下面是关于MSN Messenger这个数据集的描述:

既然是个图,则需要两个最重要的东西:
- Nodes——180M people
- Edges——1.3B edges
Degree Distribution
通过计算得到下面的度分布:

我们可以看到,数据是紧紧地贴在坐标轴上的,这不太便于我们观察,我们使用logarithmic axis[^1]来绘制图像:

Clustering

Connected Components

Diameter of WCC

Summary

我们得到了MSN的这些性质,那么这些性质是意料之中的呢?还是出乎意料的?此时,我们需要一个model来衡量,如果MSN的这些性质值与我们的model的性质值相同,那么就是意料之中的,没啥好研究,如果不同就是意料之外,值得我们研究~
接下来,我们首先用Erdös-Rényi随机图模型来衡量一下:
Erdös-Rényi随机图模型(Random Graph Model)
Erdös-Rényi随机图模型是最简单的图模型。 这个简单的模型具有经过验证的网络属性,并且是比较实际现实世界图属性的良好基准。
此随机图模型有两个变体:
- $G_{np}$: 具有 $n$ 个节点的无向图,并且每条边 $(u,v)$ 出现的概率符合概率为 $p$ 的独立同步分布;
- $G_{nm}$: 具有n个节点的无向图,随机地均匀地选择 $m$ 条边;
请注意,$G_{np}$ 和 $ G_{nm}$图不是唯一确定的,而是随机产生的。 每次生成图会产生不同的结果。
接下来,我们以$G_{np}$进行讲解,首先是计算它的度分布,距离,聚类系数和最大连接组件:
Degree Distribution of $G_{np}$
由之前$G_{np}$ 的定义,我们可以很快地得出,对于$G_{np}$中的一个顶点,它的度分布符合二项分布。
设 $P(k)$ 表示某个顶点具有度为 $k$ 的概率,则
$$
P(k)=\begin{pmatrix} n-1 \ k \ \end{pmatrix} p^{k}(1-p)^{n-1-k}
$$
二项分布的均值和方差分别为 $\bar{k}=p(n-1)$,$\sigma^{2}=p(1-p)(n-1)$。
下面,我们提供了不同参数的二项分布图。注意,二项分布与高斯的离散形式类似,并且具有钟形。

二项式分布的一个特性是,根据大数定律,随着网络规模的增加,分布变得越来越狭窄。 因此,我们越来越有信心,节点的度在 $\bar k$ 附近。 如果图具有无限个节点,则所有节点将具有相同的度数。
The Clustering Coefficient of $G_{np}$
回顾一下,聚类系数的计算公式为 $C_{i}=\frac{2e_{i}}{k_{i}(k_{i}-1)}$ 其中 $e_{i}$ 是节点 $i$ 的相邻节点之间的边数。因为在 $G_{np}$ 中边出现的概率符合概率为 $p$ 的独立同分布,所以图 $G_{np}$ 中期望的 $e_{i}$ 为 $$ \mathbb{E}\left[e_{i}\right]=p \frac{k_{i}\left(k_{i}-1\right)}{2} $$ 这是因为 $\frac {k_{i}(k_{i}-1)} {2}$ 是度为 $k_{i}$ 的节点 $i$ 的邻居的不同对的数量,并且每一对以概率 $p$ 相连接。
因此,期望的聚类系数为: $$ \mathbb{E}\left[C_{i}\right]=\frac{p \cdot k_{i}\left(k_{i}-1\right)}{k_{i}\left(k_{i}-1\right)}=p=\frac{\bar{k}}{n-1} \approx \frac{\bar{k}}{n} $$, $\bar{k}$ 表示平均度,从上面公式可以得到,$G_{np}$ 的聚类系数非常小,如果我们以固定的平均度生成 $\bar{k}$ 一个非常非常大的图,那么 $C$ 随着规模 $n$ 的增大而减小。$\mathbb{E}\left[C_{i}\right] \rightarrow 0$ as $n \rightarrow \infty$。
The Path Length of $G_{np}$
讨论 $G_{np}$ 的路径长度,我们首先介绍扩展系数的概念。
图 $G(V,E)$ 对于 $\forall S \subset V$ 具有扩展系数 $\alpha$ ,剩下的边的数量 $S \geq \alpha \cdot \min (|S|,|V \backslash S|)$。
扩展系数回答了一个问题,即“如果我们随机选择一组节点,那么至少有多少条边要离开该组?”
扩展系数是一种鲁棒性的度量:要断开 $ℓ$ 个节点,必须切断 $≥α⋅ℓ$条边。
同样的,我们也可以认为图 $G(V,E)$ 具有扩展系数
$$
\alpha=\min_{S \subset V} \frac{ # \text { edges leaving } S}{\min (|S|,|V \backslash S|)}
$$
关于扩展系数的一个重要事实是:
在具有 $n$ 个节点且扩展系数为 $α$ 的图中,对于所有的节点对,一定都会有长度为 $O((\log n)/\alpha)$ 的路径连接他们。
对于一个随机的 $G_{np}$ 图,$\log n>n p>c$,所以,$diam(G_{np})=O(\log n/ \log(np))$。
$np$表示的是average degree。
因此,我们可以看到随机图具有良好的扩展性,因此BFS访问所有节点的步数为对数。
因此 $G_{np}$ 的路径长度为 $O(\log n)$。从这个结果中,我们可以看到 $G_{np}$ 可以增长得很大,但是节点之间仍然相距几跳。
The Connectivity of $G_{np}$
下图显示了随机图 $G_{np}$ 的演变。我们可以看到当平均度 $\bar{k}=2E/n$ 或 $p=\bar{k}/(n-1)$ 时,出现了一个巨大的连通组件。如果 $k=1-\epsilon$ ,则所有组件的大小均符合 $\Omega(\log n)$。如果 $\bar{k}=1+\epsilon$ ,则存在1个连通组件的大小为 $\Omega(n)$,而所有其他组件大小都为 $\Omega(\log n)$。换句话说,如果 $\bar{k}>1$,我们希望具有一个大的连通组件。另外,在这种情况下,每个节点在期望中至少具有一条边。
当聚合系数=0的时候:也就是没有edge,这时候是一个空图
当聚合系数=1度时候:就是一个“全连接”的图
那么当聚合系数从0变化到1的过程中发生了什么变化?
【当平均度=1的时候,因为k=p(n-1),此时聚合系数c=p=1/(n-1),出现了一个大连接元,以此类推】
对比
学习完了随机图中的四个重要属性,下面来看随机图的应用性如何,看看和MSN数据的对比
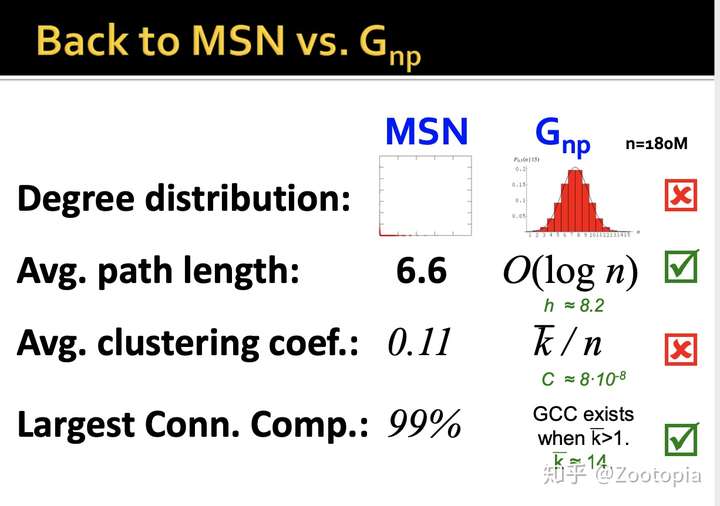
- 之前说过度分布的直方图有利于判断图的结构,MSN和随机图的直方图差距还是很大的;
- 平均路径:MSN和随机图的数据差不多
- 平均聚合系数:差距很大,随机图的非常小
- 最大连接元:很接近
综上来看,随机图的实际应用性如何?—-不好!

从上面的属性比较可以看出:实际上的网络并不是随机的。
那么问题来了,既然如此又为什么要学习随机图呢?因为这是最简单也是最有效的学习和评估网络的方法!
随机性包罗万象,我们可以根据实际网络的特性来修改随机图来适应实际网络的需要
那么,如何让随机图实际应用性变强呢?
The Small-World Model
Analyzing the Properties of $G_{np}$
在网格网络中,我们实现了三角闭合和高聚类系数,但是平均路径长度较长。
在随机网络中,我们实现了较短的平均路径长度,但聚类系数较低。
基于以上两个图结构,似乎不能直观地得到一个具有较短的平均路径长度,同时也具有较高的聚类系数的图。
但是,大多数现实世界网络具有如下表所示的属性,其中 $h$ 是平均最短路径长度,$c$ 是平均聚类系数,为了便于比较,随机图的平均度与实际网络相同。
| 网络类型 | $h_{actual}$ | $h_{random}$ | $c_{actual}$ | $c_{random}$ |
|---|---|---|---|---|
| 电影演员 | 3.65 | 2.99 | 0.79 | 0.00027 |
| 电力网络 | 18.70 | 12.40 | 0.080 | 0.005 |
| C.elegans | 2.65 | 2.25 | 0.28 | 0.05 |
同时满足以上标准的高聚类系数和小平均路径长度的网络(数学上定义为 $L\propto \log N$,其中 $L$ 是平均路径长度,$N$ 是网络中的节点的总数)称为小型世界网络。
The Small World Random Graph Model
1998年,Duncan J. Watts和Steven Strogatz提出了一个模型,该模型用于构建具有高聚类和较短平均路径长度的网络。他们将此模型称为“小世界模型”。要创建这样的模型,我们采用以下步骤:
- 从低维度的常规环开始,通过将每个节点连接到右侧的 $k$ 个邻居和左侧的 $k$ 个邻居, $k\geq2$ 。
- 通过将端点移动到随机选择的节点,以概率 $p$ 重新连接每条边(重新布线)。
然后,我们进行以下观察:
- 在 $p=0$ 没有发生重新连接边的地方,这仍然是具有高簇集,大直径的网格网络。
- 对于 $0<p<1$ ,某些边缘已经进行了重新连线,但是大部分结构仍然保留。这意味着**(localoity)和(shortcuts)**。这允许高聚类和低直径。
- 对于 $p=1$,所有边缘都进行了随机重新连接,这是一个具有低聚类,低直径的Erdős-Rényi (ER)随机图。
小世界模型通过重新连接概率 $p \in[0,1]$ 来参数化。通过观察聚类系数和平均路径长度如何随 $p$ 的变化,我们看到平均路径长度随着 $p$ 增加而下降得更快,而聚类系数仍然相对较高。重新布线引入了shortcuts,这使得在结构保持相对坚固(高度聚类)的情况下,平均路径长度也可以减小。
从社交网络的角度来看,这种现象是直观的。虽然我们的大多数朋友都是本地人,但我们在不同国家/地区也有一些远距离的友谊,这足以使人类社交网络的直径崩溃,从而解释了流行的“六度分离”概念。
Watts-Strogatz小世界模型的两个局限性在于其度的分布与现实网络的幂律分布不匹配,并且由于假定了网络的大小,因此无法对网络的增长进行建模。
The Kronecker Random Graph Model
前面一直都是在讨论随机图,上一节还说到通过对随机图引入随机“捷径”可以将随机图变为small-world model,那么这部分来讲讲如何生成大的真实图。
图生成的模型已被广泛研究。这些模型使我们能够在收集实际图困难时生成用于仿真和假设检验的图,并且还使我们可以检查生成模型应遵循的某些现实属性。
在制定图生成模型时,有两个重要的考虑因素。首先是生成现实网络的能力,其次是模型的数学易处理性,这允许对网络属性进行严格的分析。
Kronecker图模型是一个递归图生成模型,结合了数学易处理性和实际的静态和时态网络属性。Kronecker图模型的直观感受是自相似性,整体具有一个或多个部分的形状相同。
比如不同的friendship的建立往往基于相同的文化、相似的爱好等等。
Kronecker积是一种非标准的矩阵运算,是一种生成自相似矩阵的方法。
The Kronecker Product
Kronecker积使用 $\otimes$ 来表示。对于两个任意矩阵 $A \in \mathbb{R}^{m \times n}$ 和 $B \in \mathbb{R}^{p \times q}$, $A\otimes B \in \mathbb{R}^{mp \times nq}$,即:

例如,

这个积的定义基本上大家在很多数学书上都有看到,这个积的结果是明显放大了原有的矩阵的阶。那么对于在图中的推广就是利用图的邻近矩阵来做kronecker积
那么什么是kronecker 图?
答:初始图(初始邻近矩阵)的循环kronecker积。如下图,就是Kronecker图的示例:
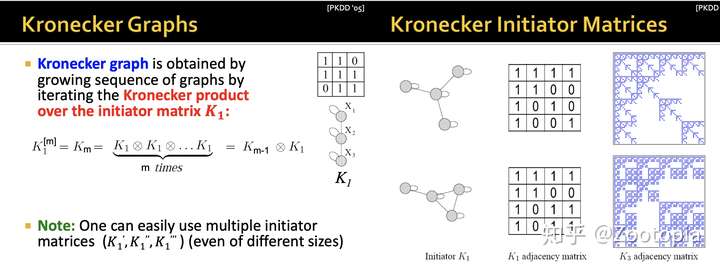
这样的方法即自然又简单,但是呢,我们观察下面这个图:
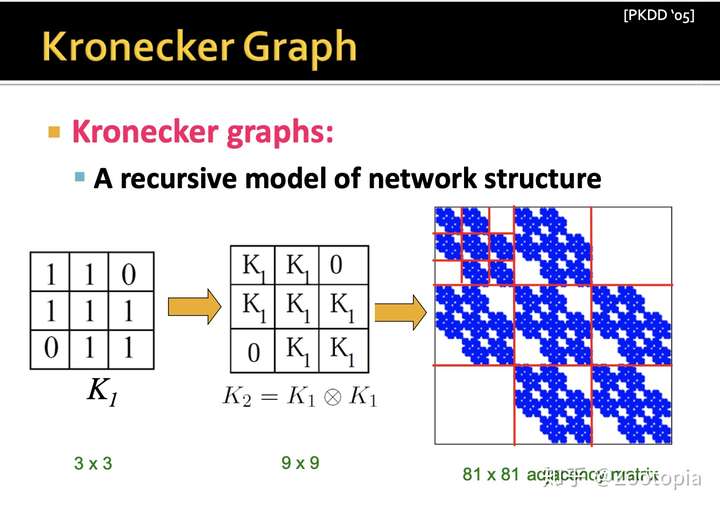
会发现得到的图邻近矩阵的结构是很规则的(因为邻近矩阵的元素都是1或者0),
类似于具有规则结构的网格一样,这样的当然好(利于我们分析),
可是这样的图结构就很难capture真实复杂网络的信息了,那么要怎么办?
-----答案是引入随机性!
这里在初始矩阵引入随机性的意思是:放松初始矩阵–邻近矩阵只有0或者1元素的条件,而是可以有[0,1]之间的元素,也就是:
(1)初始矩阵的每个元素反应的是特定边出现的概率
(2)对初始矩阵进行Kronecker积运算,以获得较大的随机邻接矩阵,在该矩阵中,大型矩阵的每个元素数值再次给出了特定边出现在大图中的概率,这样的随机邻接矩阵定义了所有图的概率分布
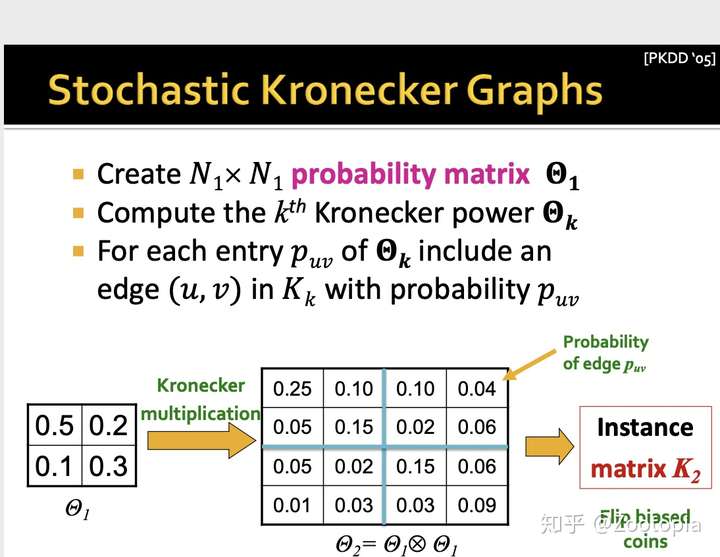
那么这个方法存在一个缺陷:费时间!
所以下面给出了一种快速方法—基于的思想:还是kronecker积的本质–循环性

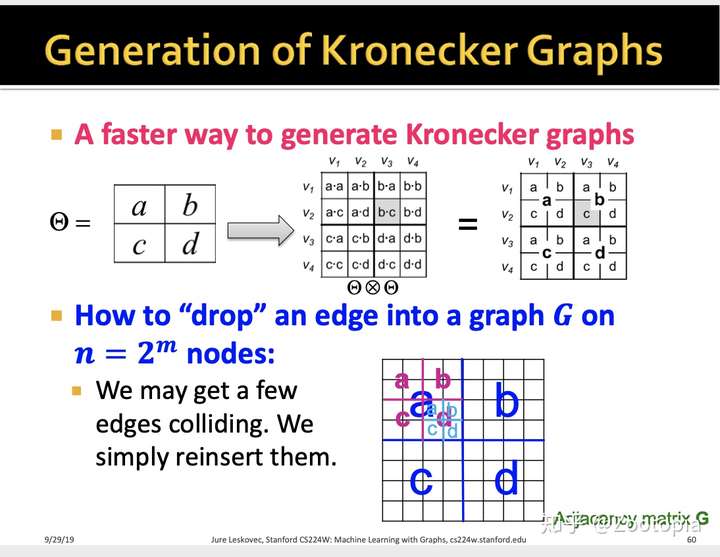

总结一下:随机kronerker图从数学上用公式来表示就是:
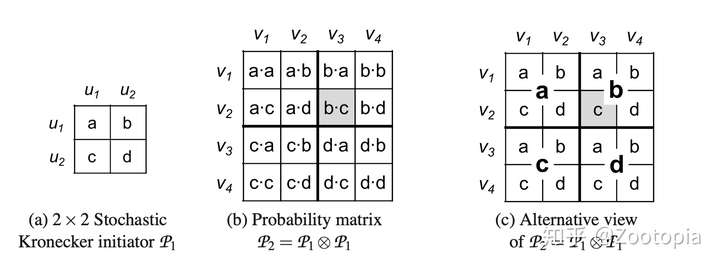
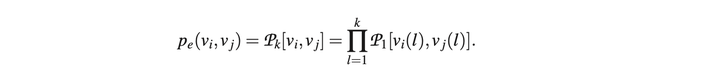
这给了我们对随机Kronecker图的非常自然的解释:每个节点由一系列分类属性值或特征来描述。然后,两个节点链接的可能性取决于各个属性相似性的乘积。
Fast Generation of Stochastic Kronecker Graphs
存在一种快速启发式生成图形的过程,该过程所需时间随着边数量线性变化。
总体思路可以描述如下:对于每个边缘,我们以概率 $p_{uv} \in \Theta_1$递归地选择大随机矩阵的子区域,直到我们下降到大随机矩阵的单个单元为止。我们将边缘放置在那里。对于Kronecker图的 $k^{th}$ 幂 $\Theta_k$,将需要 $k$ 次下降步骤。
例如,考虑 $\Theta_1$ 是一个 $2 \times 2$ 的矩阵 $$ \Theta =\begin{bmatrix} a & b \ c & d \end{bmatrix} $$ 对于具有 $n=2^k$ 个节点的图 $G$
- 创建归一化矩阵 $L_{uv}=\frac{p_{uv}}{\sum_{u,v}p_{uv}},\quad p_{uv} \in \Theta_1$
- 对于每个边缘:
- For $i=1 \dots k:$
- 初始 $x=0,y=0$
- 以概率 $L_{uv}$ 选择行和列
- 下降到 $G$ 的第 $i$ 级象限$(u,v)$
- $x=x+u \cdot 2^{k-1}$
- $y=y+v \cdot 2^{k-1}$
- 将边 $(x,y)$ 添加到 $G$
- For $i=1 \dots k:$
如果 $k=3$,且对于每一步 $i$,选择象限 $b_{(0,1)},c_{(0,1)},d_{(0,1)}$ 分别基于 $L$ 的归一化概率,有 $$ x=0\cdot 2^{3-1}+1\cdot 2^{3-2}+1\cdot 2^{3-3}=0\cdot 2^2+1\cdot 2^1+1\cdot2^{0}=3\ y=1\cdot 2^{3-1}+0\cdot 2^{3-2}+1\cdot 2^{3-3}=1\cdot 2^2+0\cdot 2^1+1\cdot2^{0}=5 $$ 因此,我们将边$(3,5)$添加到图中。
在实践中,随机Kronecker图模型能够生成与现实网络的属性非常匹配的图。要阅读有关Kronecker图模型的更多信息,请参阅 *J Leskovec et al., Kronecker Graphs: An Approach to Modeling Networks (2010)*。


