AUC在机器学习领域中是一种模型评估指标。根据维基百科的定义,AUC(area under the curve)是ROC曲线下的面积。所以,在理解AUC之前,要先了解ROC是什么。而ROC的计算又需要借助混淆矩阵,因此,我们先从混淆矩阵开始谈起。
混淆矩阵
假设,我们有一个任务:给定一些患者的样本,构建一个模型来预测肿瘤是不是恶性的。在这里,肿瘤要么良性,要么恶性,所以这是一个典型的二分类问题。
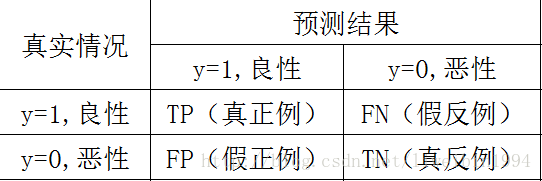
假设我们用y=1表示肿瘤是良性,y=0表示肿瘤是恶性。则我们可以制作如下图的表格:
T:True;
F:False;
P:Positive;
N:Negative;
如上图:
- TP表示预测为良性,而实际也是良性的样例数;
- FN表示预测为恶性,而实际是良性的样例数;
- FP表示预测为良性,而实际是恶性的样例数;
- TN表示预测为恶性,而实际也是恶性的样例数;
所以,上面这四个数就形成了一个矩阵,称为混淆矩阵。
那么接下来,我们如何利用混淆矩阵来计算ROC呢?
首先我们需要定义下面两个变量:
$$
FPR=\frac {FP} {FP+TN}
$$
FPR表示,在所有的恶性肿瘤中,被预测成良性的比例。称为伪阳性率。伪阳性率告诉我们,随机拿一个恶性的肿瘤样本,有多大概率会将其预测成良性肿瘤。显然我们会希望FPR越小越好。
$$
TPR=\frac {TP} {TP+FN}
$$
TPR表示,在所有良性肿瘤中,被预测为良性的比例。称为真阳性率。真阳性率告诉我们,随机拿一个良性的肿瘤样本时,有多大的概率会将其预测为良性肿瘤。显然我们会希望TPR越大越好。
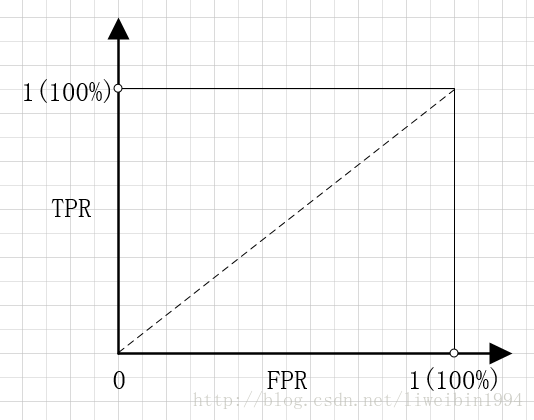
如果以FPR为横坐标,TPR为纵坐标,就可以得到下面的坐标系:
可能看到这里,你会觉得有点奇怪,用FPR和TPR分别作横纵坐标有什么用呢?我们先来考察几个特殊的点。
- 点(0,1),即FPR=0,TPR=1。FPR=0说明FP=0,也就是说,没有假正例。TPR=1说明,FN=0,也就是说没有假反例。这不就是最完美的情况吗?所有的预测都正确了。良性的肿瘤都预测为良性,恶性肿瘤都预测为恶性,分类百分之百正确。这也体现了FPR 与TPR的意义。就像前面说的我们本来就希望FPR越小越好,TPR越大越好。
- 点(1,0),即FPR=1,TPR=0。这个点与上面那个点形成对比,刚好相反。所以这是最糟糕的情况。所有的预测都预测错了。
- 点(0,0),即FPR=0,TPR=0。也就是FP=0,TP=0。所以这个点的意义是所有的样本都预测为恶性肿瘤。也就是说,无论给什么样本给我,我都无脑预测成恶性肿瘤就是了。
- 点(1,1),即FPR=1,TPR=1。显然,这个点跟点(0,0)是相反的,这个点的意义是将所有的样本都预测为良性肿瘤。
考察完这四个点,我们可以知道:
如果一个点越接近左上角,那么说明模型的预测效果越好。如果能达到左上角(点(0,1)),那就是最完美的结果了。
ROC曲线和AUC
介绍了混淆矩阵之后,我们就可以了解一下ROC(receiver operating characteristic curve)曲线是怎么定义的。
我们知道,在二分类(0,1)的模型中,一般我们最后的输出是一个概率值,表示结果是1的概率。那么我们最后怎么决定输入的x是属于0或1呢?我们需要一个阈值,超过这个阈值则归类为1,低于这个阈值就归类为0。所以,不同的阈值会导致分类的结果不同,也就是混淆矩阵不一样了,FPR和TPR也就不一样了。所以当阈值从0开始慢慢移动到1的过程,就会形成很多对(FPR, TPR)的值,将它们画在坐标系上,就是所谓的ROC曲线了。
我们来举一个例子。比如我们有5个样本:
真实的类别(label)为y = c(1,1,0,0,1).
一个分类器预测样本为1的概率为p=c(0.5, 0.6, 0.55, 0.4, 0.7)。
看到这里,也许我们还有一点难理解。这里要注意:
阈值的范围是[0,1],当阈值从1到0慢慢移动时,FPR会越来越大。因为FP(假正例)会越来越多。
如果在给定的样本中,我都随机预测,也就是0.5概率预测为良性肿瘤,0.5概率预测为恶性肿瘤。那么这条曲线会是怎样的呢?可以想象,如果数据是均匀,那么这条曲线就是y=x。
这里需要理解:为什么在随机预测的情况下,无论阈值$\alpha$取何值,
FPR和TPR一直都是相等的?- 首先,这里的随机预测表示的含义是对于
ground-truth为True的样本集,最终其样本点的预测值都是均匀分布在区间[0,1]。对于ground-truth为False的样本集同样是如此; - 因此,无论阈值$\alpha$取什么,低于$\alpha$的
groudtruth为True和groudtruth为False的样本数量应该是一样多的; - 综上,
FPR和TPR一直都是相等的。
- 首先,这里的随机预测表示的含义是对于
注意曲线一定是从(0,0)开始最终到达(1,1)的。
事实上,ROC曲线不是光滑的,而是阶梯型的。为什么呢?因为样本的数量是有限的,而FPR和TPR的变化需要至少有一个样本变化了,在没有变化的间隙里,就不会有变化。也就是说,步进是1/样本数。
理解了上面四个点的意义就知道了。
得到了ROC曲线,我们就可以计算曲线下方的面积了——计算出来的面积就是AUC值了。
AUC值的意义
知道了如何计算AUC值,我们当然是要来问一下AUC值的意义了。为什么我们要这么大费周章地搞出这个AUC值?
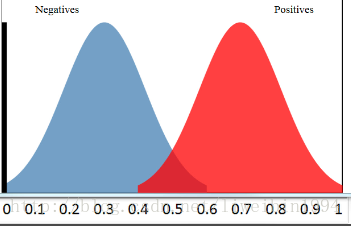
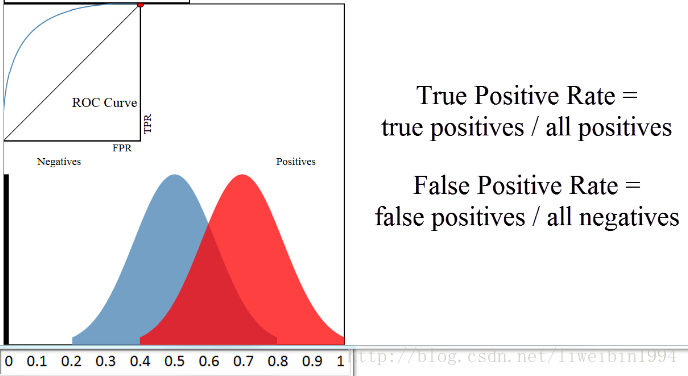
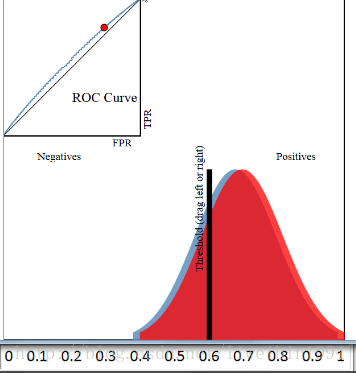
假设我们有一个分类器,输出是样本输入正例的概率,所有的样本都会有一个相应的概率,这样我们可以得到下面这个图:
其中,横轴表示预测为正例的概率,纵轴表示样本数。
所以,蓝色区域表示所有负例样本的概率分布,红色样本表示所有正例样本的概率分布。显然,如果我们希望分类效果最好的话,那么红色区域越接近1越好,蓝色区域越接近0越好。
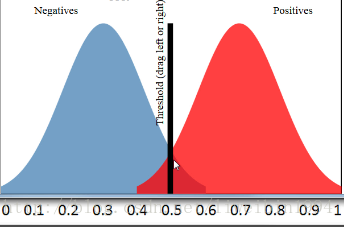
为了验证你的分类器的效果。你需要选择一个阈值,比这个阈值大的预测为正例,比这个阈值小的预测为负例。如下图:
在这个图中,阈值选择了0.5于是左边的样本都被认为是负例,右边的样本都被认为是正例。可以看到,红色区域与蓝色区域是有重叠的,所以当阈值为0.5的时候,我们可以计算出准确率为90%。
好,现在我们来引入ROC曲线。
图中左上角就是ROC曲线,其中横轴就是前面说的**FPR(False Positive Rate),纵轴就是TPR(True Positive Rate)**。
然后我们选择不同的阈值时,就可以对应坐标系中一个点。
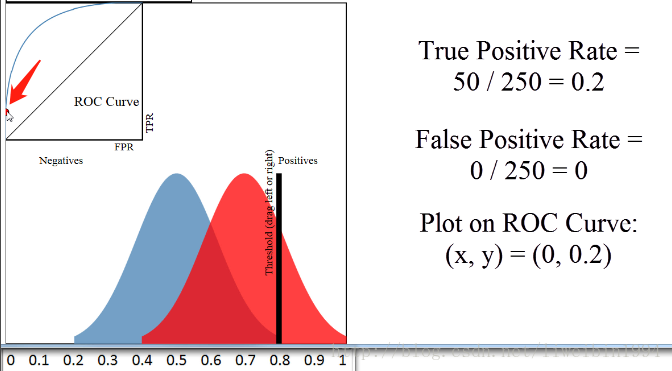
当阈值为0.8时,对应上图箭头所指的点。
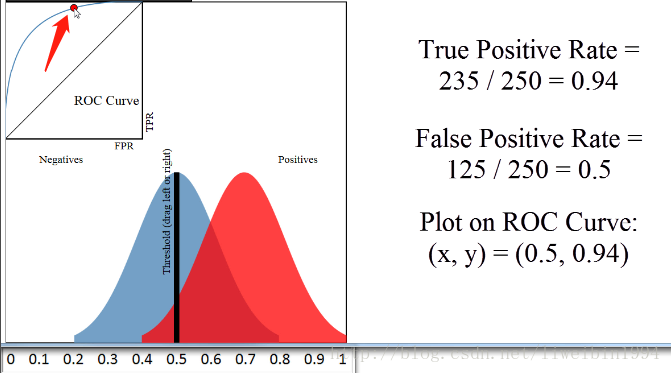
当阈值为0.5时,对应上图箭头所指的点。
这样,不同的阈值对应不同的点。最后所有的点就可以连在一起形成一条曲线,就是ROC曲线。
现在我们来看看,如果蓝色区域与红色的区域发生变化,那么ROC曲线会怎么变呢?
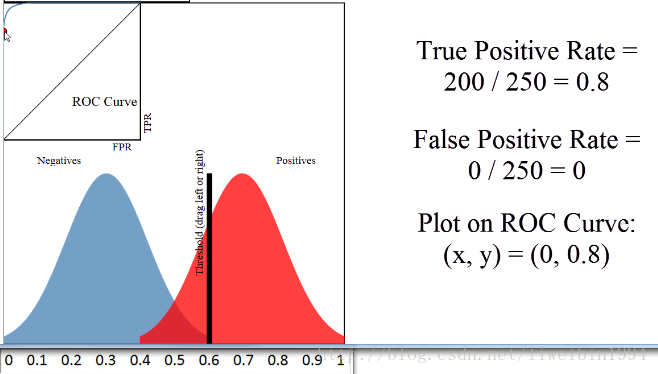
上图中,蓝色区域与红色区域的重叠部分不多,所以可以看到ROC曲线距离左上角很近。
但是,当蓝色区域与红色区域基本重叠时,ROC曲线就和接近y=x这条线了。
综上两个图,如果我们想要用ROC来评估分类器的分类质量,我们就可以通过计算AUC(ROC曲线下的面积)来评估了,这就是AUC的目的。
为什么选择ROC和AUC?
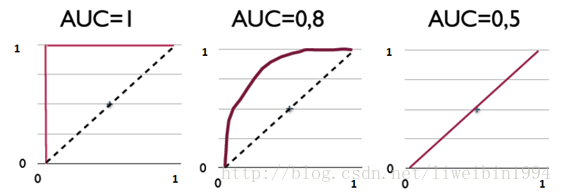
其实,AUC表示的是正例排在负例前面的百分比。
比如上图,第一个坐标系的AUC值表示,所有的正例都排在负例的前面。第二个AUC值,表示有百分之八十的正例排在负例的前面。
我们知道阈值可以取不同,也就是说,分类的结果会受到阈值的影响。如果使用AUC的话,因为阈值变动考虑到了,所以评估的效果更好。
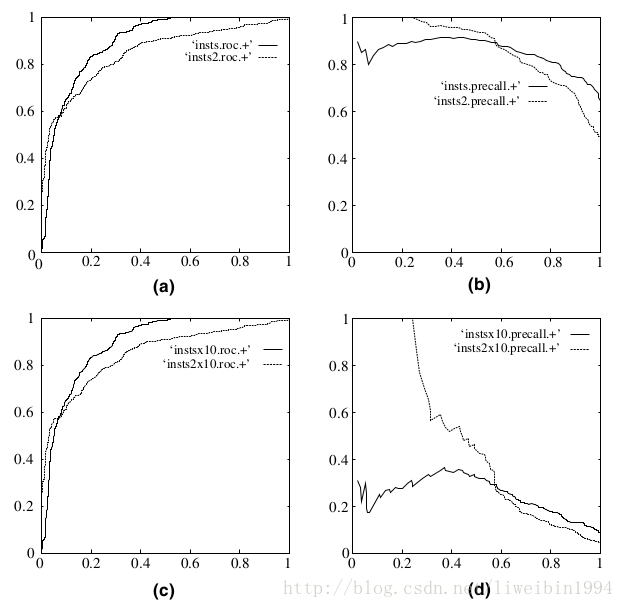
另一个好处是,ROC曲线有一个很好的特性:当测试集中的正负样本分布发生变化了,ROC曲线可以保持不变。在实际的数据集中经常会出现类不平衡(class imbalance)现象,即负样本比正样本多很多(或者相反),而且测试数据中的正负样本的分布也可能随着时间变化。
在上图中,(a)和(c)为ROC曲线,(b)和(d)为Precision-Recall曲线。(a)和(b)展示的是分类其在原始测试集(正负样本分布平衡)的结果,(c)和(d)是将测试集中负样本的数量增加到原来的10倍后,分类器的结果。可以明显的看出,ROC曲线基本保持原貌,而Precision-Recall曲线则变化较大。
参考:
https://www.zybuluo.com/frank-shaw/note/152851
https://www.zhihu.com/question/39840928?from=profile_question_card
http://blog.csdn.net/cherrylvlei/article/details/52958720
http://www.dataschool.io/roc-curves-and-auc-explained/