【斯坦福cs224w-图机器学习】7,8,9-Graph Representation Learning

GNN

发布日期: 2020-11-25

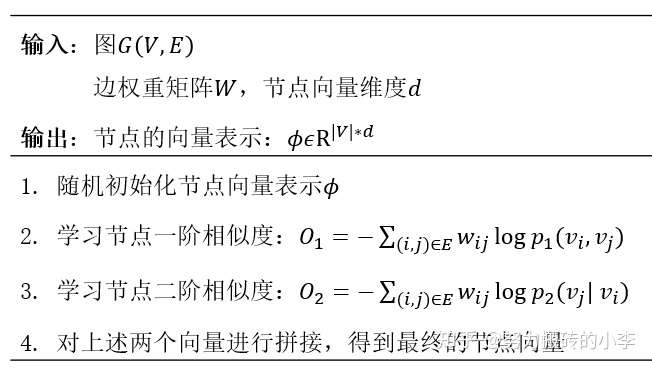
在前面几周的学习中，我们学习了motifs，graphlets等等来表示一个图，本质上，它们就是图的一种特征表示（representation），接下来我们介绍自动的方法：

第七八两节介绍的都是关于图表示学习的，所谓万物皆可embedding嘛~

第九节介绍了一些代码相关，这部分还是很建议认真看看代码找几个数据集实验一下的~

（其实介绍表示学习算法的博客已经太多太多了，但是强迫症为了笔记完整一些，还是写一写==）【ppt传送】【视频传送】

介绍分成了三个部分：

图表示学习思想
基于随机游走的表示学习（包括了DeepWalk, Node2vec, LINE)
基于深度学习的表示学习（包括了SDNE, GCN, GraphSAGE, GAT)

图表示学习思想

Embedding一直是学术界研究的热点，简单说就是利用一个低维稠密向量来对某一Object进行表示，然而在图领域，网络通常任意大小，有复杂的拓扑结构，且经常动态变化，它不像图像一样有规则的网状结构，也不像文本一样具有序列结构，而且每个节点本身也含有大量特征，所以传统的embedding方法在图数据种并不实用。

lattice：格子

img

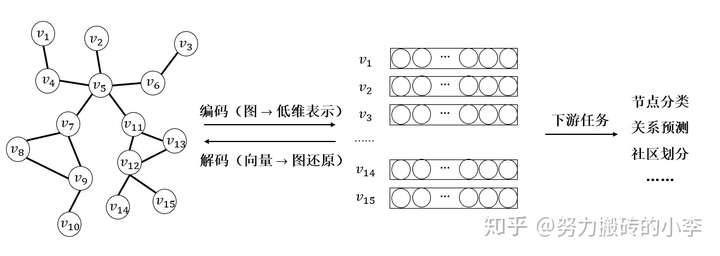
图网络问题的核心思想如下图所示，可以理解为首先把每一个节点映射为低维向量表示，并且需要保证可以重新利用某种解码方式，尽可能的还原高维空间种的图信息，比如说邻居节点之间的依赖关系，保证原有空间中节点的相似度等等。这样就可以利用到学习到的embedding用于下游任务的学习，比如说异常检测、节点分类、关系预测、社区划分、连接预测等等。

img

图表示学习大致可以分成两类：基于随机游走 & 基于深度学习

基于随机游走的表示学习

算法概览

DeepWalk：Online Learning of Social Representations
node2vec：Scalable Feature Learning for Networks
Line：Large-scale Information Network Embedding
代码：https://github.com/shenweichen/GraphEmbedding（大佬写的代码，还是很建议认真研究研究代码的~）

1. DeepWalk

DeepWalk在某种程度上是序列学习embedding在图网络中的一种迁移，它借鉴了nlp中序列的思想，可以把图中的每个节点类比为一个词语，利用随机游走出来的序列类比为一个句子，根据随机游走形成的句子序列来构建词向量模型Word2vec, 并且利用Skip-gram模型来学习每个节点的向量表示。下图为DeepWalk模型结构，分成了三个部分：随机游走采样序列；Skip-gram模型训练；输出层利用Softmax优化，最终得到每个节点的向量表示。

img

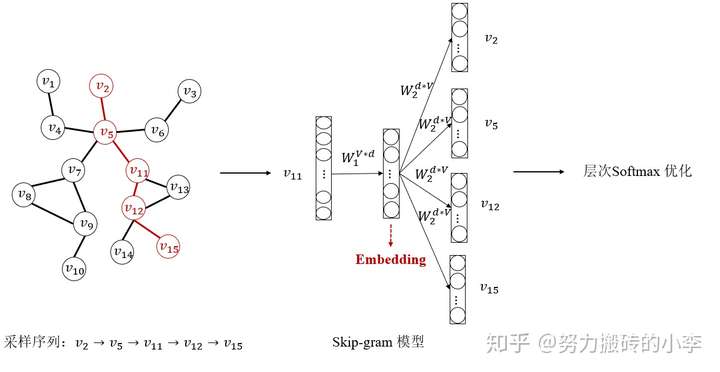
Step1：随机游走采样序列

首先定义采样次数y，每次采样的长度t，在图

$G(V,E)$

[公式]

，首先随机采样节点

$v_i$

[公式]

,然后在节点

$v_i$

[公式]

的邻居中随机采样节点

$v_j$

[公式]

,直至采样t次，生成一个采样序列，如上图所示，从节点

$v_2$

[公式]

开始，采样长度为5，生成的第一个采样序列为：

$v_2 \rightarrow v_5 \rightarrow v_{11} \rightarrow v_{12} \rightarrow v_{15}$

[公式]

，如此遍历，直至采样y次，得到了最终的采样结果。为什么要采样呢？这样利用采样后的点训练，无需关注网络中所有节点，只需要关注采样得到的序列的共现组合即可。

Step2：Skip-gram

Skip-gram 为三层的神经网络，分为输入层，映射层，输出层。核心思想是在一个序列中，利用中间节点，去预测周围的节点，对应上图的采样序列

$v_2 \rightarrow v_5 \rightarrow v_{11} \rightarrow v_{12} \rightarrow v_{15}$

[公式]

，输入为节点

$v_{11}$

[公式]

，预测周围四个节点

$v_2 ,v_5 ,v_{12},v_{15}$

[公式]

。Skip-gram 模型中输入为单词的 one-hot encoding，首先通过输入层到映射层的权重矩阵

$W_1$

[公式]

，得到中间层，然后通过映射层到输出层的权重矩阵

$W_2$

[公式]

，得到输出，输出层可用 softmax 计算，根据输出向量与真实的 one-hot 向量进行比较，根据损失函数利用反向传播算法对权重矩阵进行更新，最终的节点向量为模型的中间产物，即映射层，即当模型训练结束后，利用节点 one-hot 向量与权重矩阵

$W_1$

[公式]

相乘即可得到节点向量。

在参数求解中，上述模型等价于求解在给定节点

$v^{(t)}$

[公式]

的条件下，节点

$v^{(t j)}$

[公式]

分布的联合最大概率，即：

$max\prod_{t=1}^T\prod_{-m \leq j <m, j\neq 0}p(v^{(t j)}|v^{(t)})$

[公式]

，

等价于求解：

$min-\frac{1}{T}\sum_{t=1}^T\sum_{-m\leq j < m, j\neq 0}log p(v^{(t j)}|v^{(t)})$

[公式]

利用softmax函数有：

$p(v_o|v_c)=\frac{exp(u_o^Tw_c)}{\sum_{i\in V}exp(u_i^Tw_c)}$

[公式]

其中，

$v_c$

[公式]

为中心节点，

$v_o$

[公式]

为背景节点，

$w_c$

[公式]

为中心节点向量，

$u_o$

[公式]

为背景节点向量，取对数后求导可得：

$\frac{\partial logp(v_o|v_c)}{\partial w_c}=u_o-\sum_{j\in V}\frac{exp(u_j^Tw_c)}{\sum_{i\in V}exp(u_i^Tw_c)}u_j=u_o-\sum_{j\in V}p(v_j|v_c)u_j$

[公式]

则权重更新为：

$w_c=w_c-\frac{\partial log p(v_o|v_c)}{\partial w_c}$

[公式]

通过上述步骤，即可对Skip-gram模型中各个参数更新，进而得到每个节点的向量。

Step3：层次Softmax

上述对Skip-gram模型的参数求解的过程中，由于softmax算法在每一次参数计算与更新的过程中都引入了全部的节点，复杂度较高，为了提高算法效率，降低复杂度，就有了层次Softmax算法。

层次Softmax(Hierarchical Softmax)利用二叉树的思想，使复杂度从

$O(|V|)$

[公式]

降到

$O(|log_2V|)$

[公式]

。下图为层次Softmax的结构示意图，在输出层中引入二叉树，其中树中每一个节点代表图中一个节点，每个节点的左右子树分别为1-0，相当于二分类，则每个节点都可以通过二叉树的路径被0-1唯一编码。

img

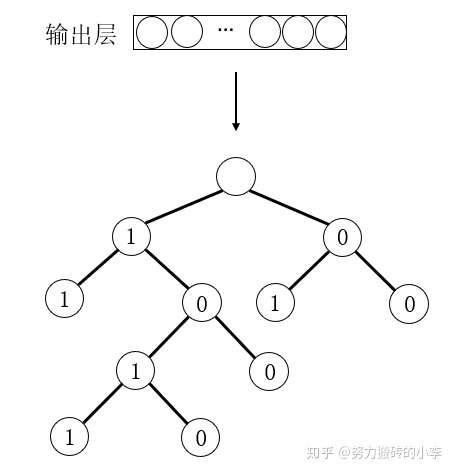
当给定背景节点来计算目标节点的条件概率

$p(v_o|v_c)$

[公式]

为：

$p(v_o|v_c)=\prod_{j=2}^{l^w}p(d_j^w|x_w, \theta_{j-1}^w)=\prod_{j=2}^{l^w}[\sigma(x_w^T\theta_{j-1}^w)]^{1-d_j^w}[1-\sigma(x_w^T\theta_{j-1}^w)]^{d_j^w}$

[公式]

其中

$l^w$

[公式]

为从根节点到目标节点中路径经过的节点个数；

$d_j^w\in\{0,1\}$

[公式]

为该节点对应的0-1编码，左子树为1，对应负类，右子树为0，对应正类；

$\theta_j^w$

[公式]

为路径中每个非叶子结点对应的向量；式中每一项为logistics回归，

$\sigma(x_w^T\theta)=\frac{1}{1 exp(-x_w^T\theta)}$

[公式]

可看作该节点被判定为正类的概率，则

$1-\sigma(x_w^T\theta)$

[公式]

为该点被判定为负类的概率；可以通过把上式代入最大似然函数求解参数。

通过上述三个步骤，就可以得到每个节点的向量表示，Deep Walk完整流程如下图所示：

img

2. Node2vec

Node2vec算法结合了深度优先搜索与广度优先搜索，利用有偏的随机游走，更好的挖掘邻居节点的特异性。DeepWalk是使邻居节点尽可能相似，但是如果两个点没有邻居，而且没有共同邻居时，也可能存在相似性，比如两个完全生活在不同时区的人，虽然互相不认识，但是也可能有相似的兴趣爱好，相似的人生轨迹，因此不仅要学习网络中位于同一社区的邻居信息，也要学习每个节点的特异性社会角色。

Node2vec与DeepWalk极为相似，关键在于随机游走的策略不同，Node2vec中结合了深度优先搜索与广度优先搜索。通过广度优先搜索，可以保持节点的结构相似性，即学习每个节点结构上扮演的角色，比如说，对于一架桥，可以直接通过它直接相连的节点识别出来；而通过深度优先搜索，可以捕捉节点的同质性，即节点之间的依赖关系，反应微观邻居的信息，随着搜索的加深，也可以捕捉更复杂的节点依赖关系。因此可以结合深度优先搜索与广度优先搜索，利用有偏的随机游走策略进行采样。

给定初始节点

$c_0=u$

[公式]

，模拟长度为l的随机游走，其中

$c_i$

[公式]

为游走中的第i个节点，则节点

$c_i$

[公式]

可由以下分布得到：

$p(c_i=x|c_{i-1}=v)=\begin{cases} \frac{\pi_{vx}}{Z},$

[公式]

其中

$\pi_{vx}$

[公式]

是节点v和节点x的转移概率，Z是归一化常数。

为了捕捉游走的回溯性与搜索方向，定义带有参数p和参数q的随机游走，如下图所示：

img

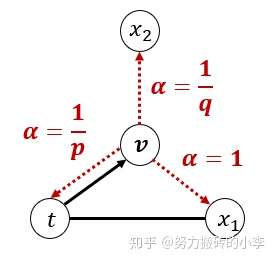
假设一个随机游走刚好经过边

$(t,v)$

[公式]

, 当前在节点v，接下来需要决定下一步，定义转移概率

$\pi_{vx}=\alpha_{pq}(t,x)w_{vx}$

[公式]

其中

$\alpha_{pq}(t,x)=\begin{cases} \frac{1}{p},$

[公式]

$d_{tx}$

[公式]

是节点t和x的最短距离。在上图中，当前节点v在下一次游走时，以概率

$w_{vx_1}$

[公式]

到达节点

$x_1$

[公式]

, 以概率

$w_{vx_2}/q$

[公式]

到达节点

$x_2$

[公式]

, 以概率

$w_{vt}/p$

[公式]

返回节点t。可以理解为参数p和q控制搜索的回溯性与搜索方向。参数p控制节点回访的概率，当

$p>1$

[公式]

时，访问之前的节点的概率就会变低，反之，当

$p<1$

[公式]

时，更可能回溯之前访问过的节点；参数q控制搜索方向，当

$q>1$

[公式]

时，倾向于游走距离节点t较近的节点，即偏向于广度优先搜索；当

$q<1$

[公式]

时，倾向于访问距离t远的节点，即倾向于深度优先搜索。

通过上述有偏的随机游走即可得到采样序列，接下来可通过与DeepWalk类似的方法利用Skip-gram进行训练，从而得到每个节点的向量表示。Node2vec的完整流程如下：

img

3. LINE

LINE其实不能算作随机游走方法，但是也经常拿来和DeepWalk，Node2vec比较。LINE的核心思想是基于近邻相似，利用一阶和二阶的相似信息和编码后向量的相似性进行比较建立损失函数，从而得到每个节点的向量表示。模型中首先定义了一阶与二阶相似性。一阶相似性是两个邻居节点的局部相似性，在一定程度上可以衡量图的局部关系。一阶相似在真实网络中很常见，比如好朋友之间有相近的兴趣爱好，引用同一篇论文的两篇文章话题相似等。然而在实际生活中，仍然有大部分不存在一阶相似性的用户，但其行为是相似的，比如两个完全不认识的人，可能因为有共同好友，而有相似的兴趣爱好，所以一阶相似度不足以表示网络结构，故引入二阶相似性，用来衡量两个节点邻居的相似性，并且认为有较多共同邻居的节点是相似的。在下图中，节点6，7有边直接相连，有较高的一阶相似度，而节点5，6虽然不直接相连，但两个节点有共同的邻居，故两节点有较高的二阶相似度。LINE分别对一阶、二阶相似度进行学习，最终把二者向量进行拼接，得到最终的节点表示。

img

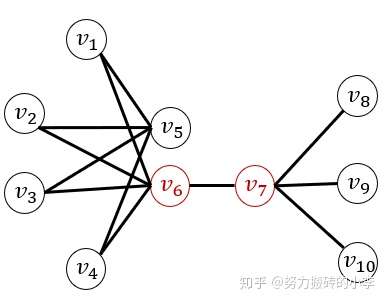
（1）一阶相似性

一阶相似度用来表示图中局部有连边的节点相似度，对于一个无向边(i,j), 定义节点

$v_i$

[公式]

和

$v_j$

[公式]

的经验概率分布为：

$\hat{p}_1(v_i,v_j)=\frac{w_{ij}}{W}$

[公式]

，其中

$w_{ij}$

[公式]

为边权，

$W=\sum_{(i,j)\in E}w_{ij}$

[公式]

当转化为低维向量时，定义其对应的联合概率分布为：

$p_1(v_i,v_j)=\frac{1}{1 exp(-\overrightarrow{u}_i^T\overrightarrow{u}_j)}$

[公式]

其中，

$\overrightarrow{u}_i\in R^d$

[公式]

为节点

$v_i$

[公式]

的低维向量表示, 因此，为了保证在转化后仍然保持高维空间中的相似关系，即需要使如下损失函数最小化：

$O_1=d(\hat{p}_1(\cdot,\cdot),p_1(\cdot, \cdot))$

[公式]

其中，

$d(\cdot, \cdot)$

[公式]

为两种分布的距离，可以利用KL散度来进行优化，即损失函数定义为：

$O_1=-\sum_{(i,j)\in E}w_{ij}logp_1(v_i,v_j)$

[公式]

通过最小化损失函数，不断迭代优化更新参数，即可得到节点的低维向量表示，但是一阶相似度只适用于无向图。

（2）二阶相似性

二阶相似度在有向图与无向图中都适用。二阶相似性认为如果两个节点有许多共同的邻居，则他们相似。在这样的假设下，每一个节点都可以看作是其他节点的“上下文”，那么有相同上下文的节点是相似的。与一阶相似度类似，对于有向图，首先定义节点

$v_i$

[公式]

和

$v_j$

[公式]

的条件概率分布为：

$\hat{p}_2(v_j|v_i)=\frac{w_{ij}}{d_i}$

[公式]

，其中，

$w_{ij}$

[公式]

为边权，

$d_i$

[公式]

为节点i的出度，即

$d_i=\sum_{k\in N(i)}w_{ik}$

[公式]

，N(i)是节点i的邻居节点。

而当转化为低维向量时，由于每个节点都有两个角色，节点本身，以及其他节点的“上下文”，因此每个节点对应两个向量，自身的向量

$\overrightarrow{u}_i$

[公式]

, 以及作为其他节点的“上下文”时的向量

$\overrightarrow{u}_l'$

[公式]

。对于一个有向边(i,j)，定义条件概率分布：

$p_2(v_j|v_i)=\frac{exp(\overrightarrow{u_j}^T\overrightarrow{u_i})}{\sum_{k=1}^{|V|}exp(\overrightarrow{u_k}^T\overrightarrow{u_i})}$

[公式]

其中|V|是每个节点的上下文个数，因此，为了保证在转化后仍然保持高维空间中的相似关系，即需要使如下损失函数最小化：

$O_2=\sum_{i\in V}\lambda_id(\hat{p}_2(\cdot|v_i),p_2(\cdot|v_i))$

[公式]

其中，

$d(\cdot, \cdot)$

[公式]

为两种分布的距离，利用参数

$\lambda_i$

[公式]

来调节不同节点的重要性，该参数可以利用节点的度，中心性，PageRank，或者模型训练得到。然后，可以利用KL散度来进行优化，即损失函数定义为：

$O_2=-\sum_{(i,j)\in E}w_{ij}logp_2(v_j|v_i)$

[公式]

通过最小化损失函数，不断迭代优化更新参数，即可得到节点的低维向量表示。

(3)模型优化

一方面，可以用负采样算法，计算开销由原来的

$O(|V|)$

[公式]

降到

$O(|K|)$

[公式]

，提高了运算效率。另外一方面，在利用梯度下降法对上述参数求解时，由于有边权重的存在，当边权重的方差较大时，对模型的扰动影响也较大，因此可以对边根据其权重大小进行采样，首先计算边权重总和，然后随机选择一个值，看其落在哪个区间中，此处利用Alias 采样方法，只需要花费常数O(1)时间，结合负采样方法，每一步只需花费

$O(dK)$

[公式]

时间，全部的复杂度为

$O(dK|E|)$

[公式]

, 其中E为边的个数。

通过上述三个步骤，则可以得到每个节点的向量表示，LINE完整流程如图所示：

img

基于深度学习的表示学习

算法概览

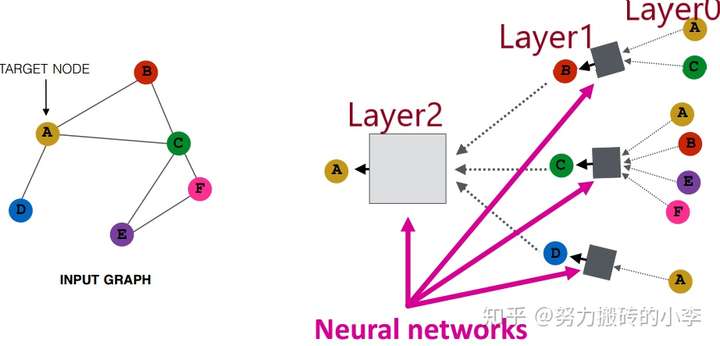
基于深度学习的图表示核心思想是对邻居节点进行聚合，如下图所示，左边是原始图网络，右图是模型的基本思想，对每个节点的邻居进行聚合，其中黑箱子可以利用不同的神经网络，此处为3层，Layer0可以输入节点特征，Layer K聚合上一层的邻居信息。基础的模型为：

$\begin{align} h_v^0$

[公式]

此处利用了上一层邻居的平均来进行聚合，

$W_k$

[公式]

和

$B_k$

[公式]

是要学习的参数，可以利用无监督和有监督的方法学习参数。由于聚合参数在所有节点中是共享的，所以此方法可以快速泛化到训练中未出现过的节点中

img

SDNE

SDNE(Structural Deep Network Embedding)将深度学习用于网络表示，利用非线性映射保留网络结构，也可以看作是一种自编码器，其中与LINE类似，利用一阶相似度保存临近节点之间的局部相似关系，利用二阶相似度保存每对节点的邻居节点间的相似度从而保存全局网络结构，通过这样的编码-解码利用非线性函数把输入转化到表示空间。

下图为SDNE的模型结构，核心框架是自编码器Encoder-Decoder, 首先对输入的节点进行编码，保存到y，然后再对y进行解码，尽可能的还原原始输入，其中根据一阶相似度与二阶相似度建立损失函数，通过最小化损失函数来进行参数更新，从而得到节点的低维向量表示。

img

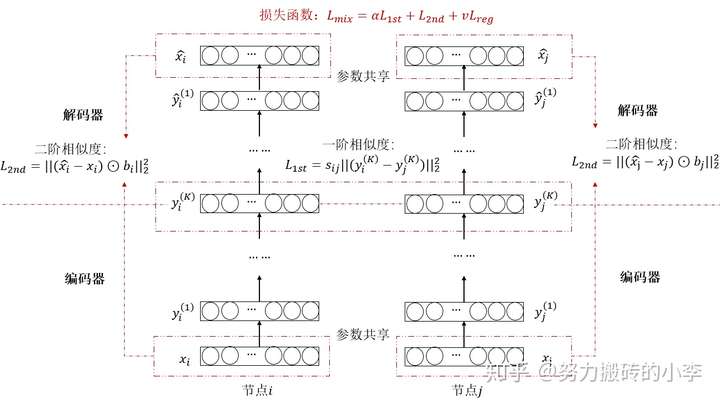
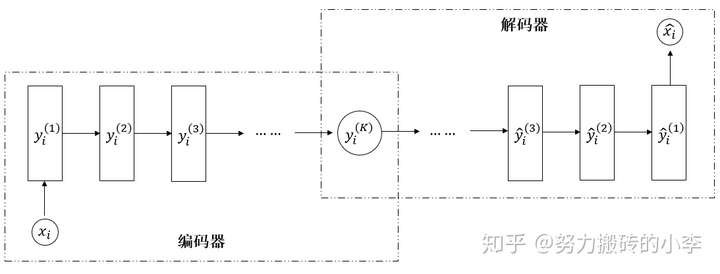
（1）自编码器Encoder-Decoder

如下图所示，在编码器Encoder中，对输入节点x进行编码，经历K层，存储在背景向量

$y_i^{(K)}$

[公式]

中，背景向量

$y_i^{(K)}$

[公式]

尽可能保留了原始输入节点的信息，然后将背景向量

$y_i^{(K)}$

[公式]

作为解码器Decoder的输入，建立模型还原初始输入x。

img

（2）一阶相似度

为了捕捉图相邻节点的局部的相似结构，认为有直接相连的节点之间是相似的，利用编码后的临近节点有监督学习其一阶相似度：

$L_{1st}=\sum_{i,j=1}^ns_{ij}||y_i^{(K)}-y_j^{(K)}||_2^2=\sum_{i,j=1}^ns_{ij}||y_i-y_j||^2_2$

[公式]

其中S为邻接矩阵，代表邻居的结构。

（3）二阶相似度

一阶相似度可以使有邻居节点有相似的向量表示，但是不连接并不能代表没有相似性，因此希望通过自编码器，可以尽可能的还原初始的网络结构，即保持网络全局的结构，建立损失函数：

$L_{2nd}=\sum_{i=1}^n||\hat{x}_i-x_i||^2_2$

[公式]

然而，邻接矩阵中0是大部分，把所有函数学成0不是理想的结果，因此可以对非零元素进行惩罚建立带权的损失函数：

$L_{2nd}=\sum_{i=1}^n||(\hat{x}_i-x_i)\odot b_i||^2_2=||(\hat{X}-X)\odot B||^2_2$

[公式]

其中

$b_{ij}=\begin{cases} 1,$

[公式]

。

综上所述，可以优化目标函数：

$\begin{align} L_{mix}$

[公式]

对其中的参数利用梯度下降法进行求解，从而得到每个节点的向量表示。通过结合一阶相似度与二阶相似度，既保留了相似邻居的局部信息，也保留了网络结构的全局信息。SDNE的完整流程如下：

img

2. GCN

GCN的细节原理关于卷积核，傅里叶变化，拉普拉斯分解细究起来确实复杂，感兴趣的可以参考这里，此处只不求甚解说结论好了，GCN可以理解为一种神经网络，用一种特殊的编码方式捕捉图信息，如下图所示为两层的图卷积网络，利用所有数据学习节点表示，并利用有标签的数据建立损失函数，半监督对节点进行分类。

img

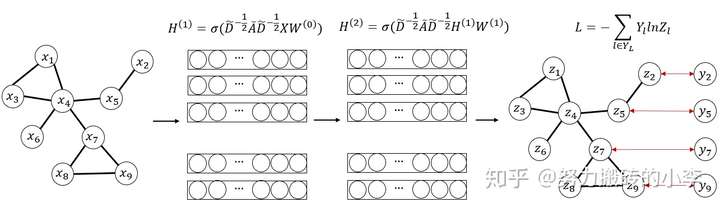
其层与层之间的传播规则为：

$H^{(l 1)}=\sigma(\widetilde{D}^{-\frac{1}{2}}\widetilde{A}\widetilde{D}^{-\frac{1}{2}}H^{(l)}W^{(l)})$

[公式]

，其中

$\widetilde{A}=A I_N$

[公式]

是邻接矩阵加上自身单位矩阵，

$\widetilde{D}_{ii}=\sum_j\widetilde{A}_{ij}$

[公式]

为度矩阵，

$W^{(l)}$

[公式]

是每一层待训练的参数，H是每一层的特征，初始为图的特征矩阵，

$\widetilde{D}^{-\frac{1}{2}}\widetilde{A}\widetilde{D}^{-\frac{1}{2}}$

[公式]

为对邻接矩阵的归一化，是谱图卷积的核心。

（对比最开始提到的，对邻居节点进行均值聚合

$\sum_{u\in N(v)}\frac{h_u^{k-1}}{|N(v)|}$

[公式]

和

$H^k=D^{-1}AH^{k-1}$

[公式]

等价，可以理解为GCN是对神经网络的一种堆叠，来平均邻居信息）

通过上式后就可以利用损失函数（监督/无监督）来对参数进行更新学习，得到每个节点的向量表示。

3. GraphSAGE

GraphSAGE全称为Graph sample and aggregate，对比深度学习表示学习最开始提到的核心思想对邻居简单聚合，GraphSAGE的聚合更加泛化。

简单邻居聚合：
$h_v^k=\sigma(W_k\sum_{u\in N(v)}\frac{h_u^{k-1}}{|N(v)|} B_kh_v^{k-1})$
[公式]
GraphSAGE聚合：
$h_v^k=\sigma([W_k\cdot AGG(\{h_u^{k-1},\forall u\in N(v)\}), B_kh_v^{k-1}])$
[公式]

其中对于函数AGG有多种选择，比如说：

均值聚合：
$AGG=\sum_{u\in N(v)}\frac{h_u^{k-1}}{|N(v)|}$
[公式]
池化聚合：
$AGG=\gamma (\{Wh_u^{k-1},\forall u\in N(v)\})$
[公式]
，其中
$\gamma$
[公式]
为max pool/mean pool
LSTMuh聚合：
$AGG=LSTM([h_u^{k-1}, \forall u\in \pi (N(v))])$
[公式]

GraphSAGE的完整流程如图所示：

img

4. Graph Attention Networks（GAT）

在GraphSAGE中认为，邻居节点对当前节点的影响是相同的，而GAT引入注意力机制，对不同的邻居节点赋予不同的权重

Step1：对于图中每个节点，通过线性映射定义节点u对节点v的重要性：
$e_{vu}=a(W_kh_u^{k-1}, W_kh_v^{k-1})$
[公式]
Step2：计算注意力得分：
$\alpha_{vu}=\frac{exp(e_{vu})}{\sum_{k\in N(v)}exp(e_{vk})}$
[公式]
Step3：得到最终的隐藏层：
$h_v^k=\sigma(\sum_{u\in N(v)}\alpha_{vu}W_kh_u^{k-1})$
[公式]