原文地址:Numpy:对Axis的理解
- Axis就是数组层级
- 设axis=i,则Numpy沿着第i个下标变化的方向进行操作
- Axis的应用
Axis就是数组层级
要想理解axis,首先我们先要弄清楚“Numpy中数组的维数”和”线性代数中矩阵的维数”这两个概念以及它们之间的关系。在数学或者物理的概念中,dimensions被认为是在空间中表示一个点所需要的最少坐标个数,但是在Numpy中,dimensions指代的是数组的维数。比如下面这个例子:
>>> import numpy as np
>>> a = np.array([[1,2,3],[2,3,4],[3,4,9]])
>>> a
array([[1, 2, 3],
[2, 3, 4],
[3, 4, 9]])
这个array的维数只有2,即axis轴有两个,分别是axis=0和axis=1。如下图所示,该二维数组的第0维(axis=0)有三个元素(左图),即axis=0轴的长度length为3;第1维(axis=1)也有三个元素(右图),即axis=1轴的长度length为3。正是因为axis=0、axis=1的长度都为3,矩阵横着竖着都有3个数,所以该矩阵在线性代数是3维的(rank秩为3)。
因此,axis就是数组层级。
当axis=0,该轴上的元素有3个(数组的size为3)
a[0]、a[1]、a[2]
当axis=1,该轴上的元素有3个(数组的size为3)
a[0][0]、a[0][1]、a[0][2]
(或者a[1][0]、a[1][1]、a[1][2])
(或者a[2][0]、a[2][1]、a[2][2])
再比如下面shape为(3,2,4)的array:
>>> b = np.array([[[1,2,3,4],[1,3,4,5]],[[2,4,7,5],[8,4,3,5]],[[2,5,7,3],[1,5,3,7]]])
>>> b
array([[[1, 2, 3, 4],
[1, 3, 4, 5]],
[[2, 4, 7, 5],
[8, 4, 3, 5]],
[[2, 5, 7, 3],
[1, 5, 3, 7]]])
>>> b.shape
(3, 2, 4)
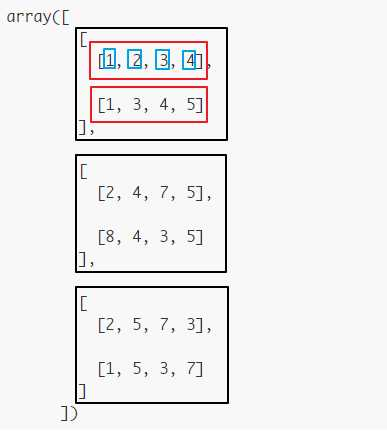
这个shape(用tuple表示)可以理解为在每个轴(axis)上的size,也即占有的长度(length)。为了更进一步理解,我们可以暂时把多个axes想象成多层layers。axis=0表示第一层(下图黑色框框),该层数组的size为3,对应轴上的元素length = 3;axis=1表示第二层(下图红色框框),该层数组的size为2,对应轴上的元素length = 2;axis=2表示第三层(下图蓝色框框),对应轴上的元素length = 4。
设axis=i,则Numpy沿着第i个下标变化的方向进行操作
1. 二维数组示例:
比如np.sum(a, axis=1),结合下面的数组, a[0][0]=1、a[0][1]=2、a[0][2]=3 ,下标会发生变化的方向是数组的第一维。
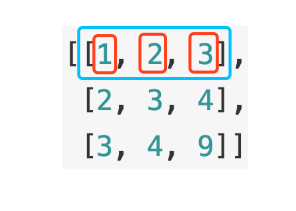
我们往下标会变化的方向,把元素相加后即可得到最终结果:
[
[6],
[9],
[16]
]
2. 三维数组示例:
再举个例子,比如下边这个np.shape(a)=(3,2,4)的3维数组,该数组第0维的长度为3(黑色框框),再深入一层,第1维的长度为2(红色框框),再深入一层,第2维的长度为4(蓝色框框)。
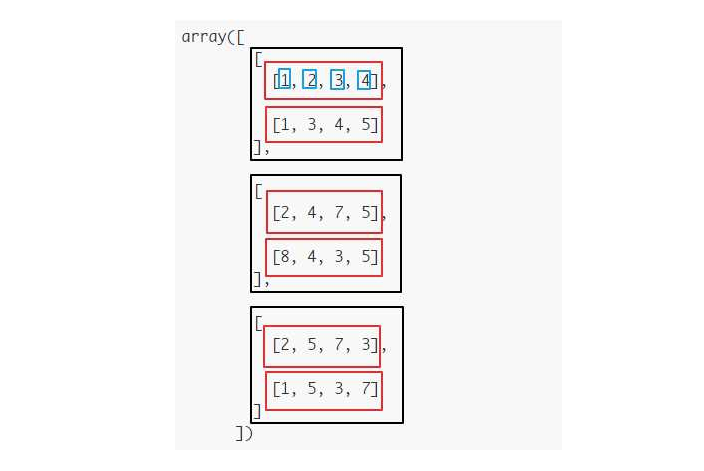
如果我们要计算np.sum(a, axis=1),在第一个黑色框框中,
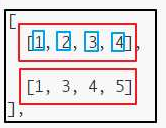
下标的变化方向如下所示:

需要注意的是,不变的部分就是新的数组的下标,例如上图将形成新数组的
[0][0],[0][1]、[0][2]元素~
按照同样的逻辑处理第二个和第三个黑色的框框,可以得出最终结果:
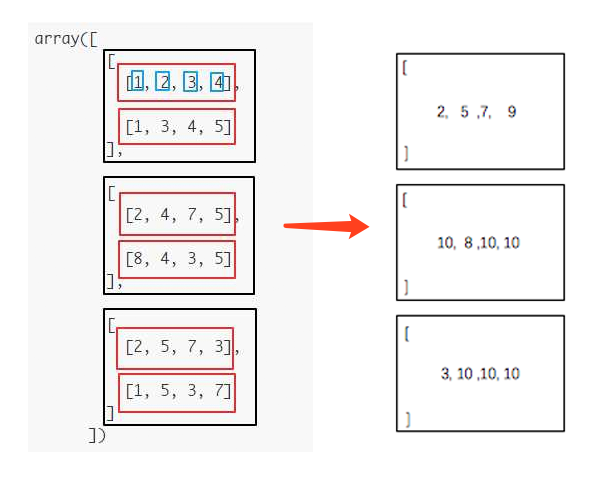
所以,依然是我们前边总结的那一句话,设axis=i,则Numpy沿着第i个下标变化的方向进行操作。
3. 四维数组示例:
比如下面这个巨复杂的4维数组,
>>> data = np.random.randint(0, 5, [4,3,2,3])
>>> data
array([[[[4, 1, 0],
[4, 3, 0]],
[[1, 2, 4],
[2, 2, 3]],
[[4, 3, 3],
[4, 2, 3]]],
[[[4, 0, 1],
[1, 1, 1]],
[[0, 1, 0],
[0, 4, 1]],
[[1, 3, 0],
[0, 3, 0]]],
[[[3, 3, 4],
[0, 1, 0]],
[[1, 2, 3],
[4, 0, 4]],
[[1, 4, 1],
[1, 3, 2]]],
[[[0, 1, 1],
[2, 4, 3]],
[[4, 1, 4],
[1, 4, 1]],
[[0, 1, 0],
[2, 4, 3]]]])
当axis=0时,numpy沿着第0维的方向进行求和,也就是第一个元素值=a0000+a1000+a2000+a3000=11,第二个元素=a0001+a1001+a2001+a3001=5,同理可得最后的结果如下:
>>> data.sum(axis=0)
array([[[11, 5, 6],
[ 7, 9, 4]],
[[ 6, 6, 11],
[ 7, 10, 9]],
[[ 6, 11, 4],
[ 7, 12, 8]]])
当axis=3时,numpy沿着第3维的方向进行求和,也就是第一个元素值=a0000+a0001+a0002=5,第二个元素=a0010+a0011+a0012=7,同理可得最后的结果如下:
>>> data.sum(axis=3)
array([[[ 5, 7],
[ 7, 7],
[10, 9]],
[[ 5, 3],
[ 1, 5],
[ 4, 3]],
[[10, 1],
[ 6, 8],
[ 6, 6]],
[[ 2, 9],
[ 9, 6],
[ 1, 9]]])
Axis的应用
例如现在我们收集了四个同学对苹果、榴莲、西瓜这三种水果的喜爱程度进行打分的数据(总分为10),每个同学都有三个特征:
>>> item = np.array([[1,4,8],[2,3,5],[2,5,1],[1,10,7]])
>>> item
array([[1, 4, 8],
[2, 3, 5],
[2, 5, 1],
[1, 10, 7]])
每一行包含了同一个人的三个特征,如果我们想看看哪个同学最喜欢吃水果,那就可以用:
>>> item.sum(axis=1)
array([13, 10, 8, 18])
可以大概看出来同学4最喜欢吃水果。
如果我们想看看哪种水果最受欢迎,那就可以用:
>>> item.sum(axis = 0)
array([ 6, 22, 21])
可以看出基本是榴莲最受欢迎。


