多分类，多标签模型的Accuracy, Precision, Recall和F1-score

机器学习

发布日期: 2020-12-11

前言

众所周知，机器学习分类模型常用评价指标有Accuracy, Precision, Recall和F1-score，而回归模型最常用指标有MAE和RMSE。但是我们真正了解这些评价指标的意义吗？

在具体场景（如不均衡多分类）中到底应该以哪种指标为主要参考呢？多分类模型和二分类模型的评价指标有啥区别？多分类问题中，为什么Accuracy = micro precision = micro recall = micro F1-score? 什么时候用macro, weighted, micro precision/ recall/ F1-score?

这几天为了回复严谨（划去: 刁难）的reviewer，我查阅了一些文章，总算是梳理清楚啦。在这里分享给大家，权当做个总结。今天要讲的主要分为以下两点：

二分类模型的常见指标快速回顾
多分类模型的常见指标详细解析
多标签模型的常见指标详细解析

在探讨这些问题前，让我们先回顾一下最常见的指标Accuracy到底有哪些不足。

Accuracy是分类问题中最常用的指标，它计算了分类正确的预测数与总预测数的比值。但是，对于不平衡数据集而言，Accuracy并不是一个好指标。为啥？

假设我们有100张图片，其中91张图片是「狗」，5张是「猫」，4张是「猪」，我们希望训练一个三分类器，能正确识别图片里动物的类别。其中，狗这个类别就是大多数类 (majority class)。当大多数类中样本（狗）的数量远超过其他类别（猫、猪）时，如果采用Accuracy来评估分类器的好坏，那么即便模型性能很差 (如无论输入什么图片，都预测为「狗」)，也可以得到较高的Accuracy Score（如91%）。此时，虽然Accuracy Score很高，但是意义不大。当数据异常不平衡时，Accuracy评估方法的缺陷尤为显著。

因此，我们需要引入Precision （精准度），Recall （召回率）和F1-score评估指标。考虑到二分类，多分类，多标签模型中，评估指标的计算方法略有不同，我们将其分开讨论。

二分类模型的常见指标快速回顾

在二分类问题中，假设该样本一共有两种类别：Positive和Negative。当分类器预测结束，我们可以绘制出混淆矩阵（confusion matrix）。其中分类结果分为如下几种：

True Positive (TP): 把正样本成功预测为正。
True Negative (TN)：把负样本成功预测为负。
False Positive (FP)：把负样本错误地预测为正。
False Negative (FN)：把正样本错误的预测为负。

在二分类模型中，Accuracy，Precision，Recall和F1 score的定义如下：

$Accuracy = \frac{TP TN}{TP TN FP FN}$

$Precision = \frac{TP}{TP FP}$

$Recall = \frac{TP}{TP FN}$

$F1\text{-}score = \frac{2\times \text{Precision} \times \text{Recall}}{ \text{Precision} \text{Recall}}$

F1-score的计算方式在数学中称为：调和平均。

其中，Precision着重评估在预测为Positive的所有数据中，真实Positve的数据到底占多少？Recall着重评估：在所有的Positive数据中，到底有多少数据被成功预测为Positive?

举个例子，一个医院新开发了一套癌症AI诊断系统，想评估其性能好坏。我们把病人得了癌症定义为Positive，没得癌症定义为Negative。那么，到底该用什么指标进行评估呢？

如用Precision对系统进行评估，那么其回答的问题就是：

在诊断为癌症的一堆人中，到底有多少人真得了癌症？

如用Recall对系统进行评估，那么其回答的问题就是：

在一堆得了癌症的病人中，到底有多少人能被成功检测出癌症？

如用Accuracy对系统进行评估，那么其回答的问题就是：

在一堆癌症病人和正常人中，有多少人被系统给出了正确诊断结果（患癌或没患癌）？

OK，那啥时候应该更注重Recall而不是Precision呢？

当False Negative (FN)的成本代价很高 (后果很严重)，希望尽量避免产生FN时，应该着重考虑提高Recall指标。

在上述例子里，False Negative是得了癌症的病人没有被诊断出癌症，这种情况是最应该避免的。我们宁可把健康人误诊为癌症 (FP)，也不能让真正患病的人检测不出癌症 (FN) 而耽误治疗离世。在这里，癌症诊断系统的目标是：尽可能提高Recall值，哪怕牺牲一部分Precision。

那啥时候应该更注重Precision而不是Recall呢？

当False Positive (FP)的成本代价很高 (后果很严重)时，即期望尽量避免产生FP时，应该着重考虑提高Precision指标。

以垃圾邮件屏蔽系统为例，垃圾邮件为Positive，正常邮件为Negative，False Positive是把正常邮件识别为垃圾邮件，这种情况是最应该避免的（你能容忍一封重要工作邮件直接进了垃圾箱，被不知不觉删除吗？）。我们宁可把垃圾邮件标记为正常邮件 (FN)，也不能让正常邮件直接进垃圾箱 (FP)。在这里，垃圾邮件屏蔽系统的目标是：尽可能提高Precision值，哪怕牺牲一部分recall。

而F1-score是Precision和Recall两者的综合。

举个更有意思的例子（我拍脑袋想出来的，绝对原创哈），假设检察机关想将罪犯捉拿归案，需要对所有人群进行分析，以判断某人犯了罪（Positive），还是没犯罪（Negative）。显然，检察机关希望不漏掉一个罪人（提高recall），也不错怪一个好人（提高precision），所以就需要同时权衡recall和precision两个指标。

尤其在上个世纪，中国司法体制会更偏向Recall，即「天网恢恢，疏而不漏，任何罪犯都插翅难飞」。而西方司法系统会更偏向Precision，即「绝不冤枉一个好人，但是难免有罪犯成为漏网之鱼，逍遥法外」。到底是哪种更好呢？显然，极端并不可取。Precision和Recall都应该越高越好，也就是F1应该越高越好。

呼，二分类问题的常见指标和试用场景终于讲完了。咦，说好的快速回顾呢？

多分类模型的常见指标详细解析

在多分类（大于两个类）问题中，假设我们要开发一个动物识别系统，来区分输入图片是猫，狗还是猪。给定分类器一堆动物图片，产生了如下结果混淆矩阵。

在混淆矩阵中，正确的分类样本（Actual label = Predicted label）分布在左上到右下的对角线上。其中，Accuracy的定义为分类正确（对角线上）的样本数与总样本数的比值。Accuracy度量的是全局样本预测情况。而对于Precision和Recall而言，每个类都需要单独计算其Precision和Recall。

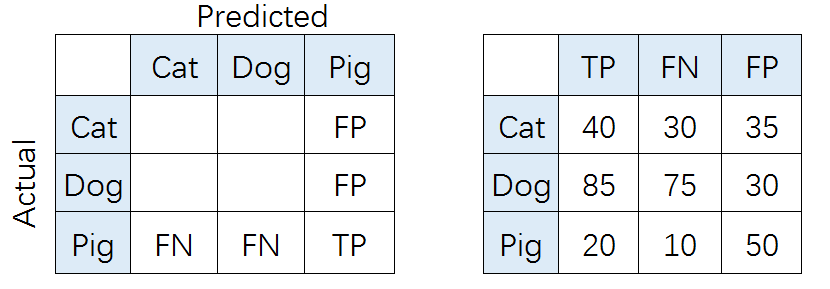
比如，对类别「猪」而言，其Precision和Recall分别为:

$Precision = \frac{TP}{TP FP} = \frac{20}{20 50} = 2/7$

$Recall = \frac{TP}{TP FN} = \frac{20}{20 10} = 2/3$

也就是，

$P_{cat}=8/15, P_{dog} = 17/23,P_{pig}=2/7$ （P代表Precision）

$R_{cat}=4/7, R_{dog} = 17/32,R_{pig}=2/3$ （R代表Recall）

如果想评估该识别系统的总体功能，必须考虑猫、狗、猪三个类别的综合预测性能。那么，到底要怎么综合这三个类别的Precision呢？是简单加起来做平均吗？通常来说，我们有如下几种解决方案（也可参考scikit-learn官网）：

1. Macro-average方法

该方法最简单，直接将不同类别的评估指标（Precision/ Recall/ F1-score）加起来求平均，给所有类别相同的权重。该方法能够平等看待每个类别，但是它的值会受稀有类别影响。

$\text{Macro-Precision} = \frac{{P}_{cat} P_{dog} P_{pig} }{3} = 0.5194$

$\text{Macro-Recall} = \frac{R_{cat} R_{dog} R_{pig} }{3} = 0.5898$

2. Weighted-average方法

该方法给不同类别不同权重（权重根据该类别的真实分布比例确定），每个类别乘权重后再进行相加。该方法考虑了类别不平衡情况，它的值更容易受到常见类（majority class）的影响。

$\text{W}_{cat} : \text{W}_{dog} : \text{W}_{pig} = \text{N}_{cat} : \text{N}_{dog} :\text{N}_{pig} = \frac{7}{26} : \frac{16}{26}: \frac{3}{26}$ (W代表权重，N代表样本在该类别下的真实数目)

$\text{Weighted-Precision} = {P}_{cat}\times W_{cat} {P}_{dog}\times W_{dog} {P}_{pig}\times W_{pig} = 0.6314$

$\text{Weighted-Recall} = {R}_{cat}\times W_{cat} {R}_{dog}\times W_{dog} {R}_{pig}\times W_{pig} = 0.5577$

3. Micro-average方法

该方法把每个类别的TP, FP, FN先相加之后，在根据二分类的公式进行计算。

$\text{Micro-Precision} = \frac{{TP}_{cat} {TP}_{dog} {TP}_{pig}}{ {TP}_{cat} {TP}_{dog} {TP}_{pig} {FP}_{cat} {FP}_{dog} {FP}_{pig}} = 0.5577$

$\text{Micro-Recall} = \frac{{TP}_{cat} {TP}_{dog} {TP}_{pig}}{ {TP}_{cat} {TP}_{dog} {TP}_{pig} {FN}_{cat} {FN}_{dog} {FN}_{pig}}=0.5577$

其中，特别有意思的是，Micro-precision和Micro-recall竟然始终相同！这是为啥呢？

这是因为在某一类中的False Positive样本，一定是其他某类别的False Negative样本。听起来有点抽象？举个例子，比如说系统错把「狗」预测成「猫」，那么对于狗而言，其错误类型就是False Negative，对于猫而言，其错误类型就是False Positive。于此同时，Micro-precision和Micro-recall的数值都等于Accuracy，因为它们计算了对角线样本数和总样本数的比值，总结就是：

$\text{Micro-Precision} = \text{Micro-Recall} = \text{Micro-F1 score} = \text{Accuracy}$

最后，我们运行一下代码，检验手动计算结果是否和Sklearn包结果一致：

import numpy as np
import seaborn as sns
from sklearn.metrics import confusion_matrix
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.metrics import accuracy_score, average_precision_score,precision_score,f1_score,recall_score

# create confusion matrix
y_true = np.array([-1]*70 + [0]*160 + [1]*30)
y_pred = np.array([-1]*40 + [0]*20 + [1]*20 + 
                  [-1]*30 + [0]*80 + [1]*30 + 
                  [-1]*5 + [0]*15 + [1]*20)
cm = confusion_matrix(y_true, y_pred)
conf_matrix = pd.DataFrame(cm, index=['Cat','Dog','Pig'], columns=['Cat','Dog','Pig'])

# plot size setting
fig, ax = plt.subplots(figsize = (4.5,3.5))
sns.heatmap(conf_matrix, annot=True, annot_kws={"size": 19}, cmap="Blues")
plt.ylabel('True label', fontsize=18)
plt.xlabel('Predicted label', fontsize=18)
plt.xticks(fontsize=18)
plt.yticks(fontsize=18)
plt.savefig('confusion.pdf', bbox_inches='tight')
plt.show()

print('-----Macro-----')
print('Macro precision',precision_score(y_true,y_pred,average='macro'))
print('Macro recall',recall_score(y_true,y_pred,average='macro'))
print('Macro f1-score',f1_score(y_true,y_pred,average='macro'))

print('-----Weighted-----')
print('Weighted precision',precision_score(y_true,y_pred,average='weighted'))
print('Weighted recall',recall_score(y_true,y_pred,average='weighted'))
print('Weighted f1-score',f1_score(y_true,y_pred,average='weighted'))

print('-----Micro-----')
print('Micro precision',precision_score(y_true,y_pred,average='micro'))
print('Micro recall',recall_score(y_true,y_pred,average='micro'))
print('Micro f1-score',f1_score(y_true,y_pred,average='micro'))

-----Macro-----
Macro precision 0.5193926846100759
Macro recall 0.589781746031746
Macro f1-score 0.5233019853709507
-----Weighted-----
Weighted precision 0.6314062748845358
Weighted recall 0.5576923076923077
Weighted f1-score 0.575114540631782
-----Micro-----
Micro precision 0.5576923076923077
Micro recall 0.5576923076923077
Micro f1-score 0.5576923076923077

运算结果完全一致。

多标签模型的常见指标详细解析

前面讲解了二分类和多分类模型的评价指标，那么对于多标签分类模型，它的评价指标又是怎么计算的呢？

在针对multilabel分类计算F score的时候，通常有macro和micro两种average的方法。Python的scikit-learn库在计算f1 score也提供了micro和macro两种选择，具体在multilabel的情况下，怎么计算F1-score，在网上查阅了很多博客和资料都没有给出一个明确的用列子解释的步骤，这边我自己通过整合资料代码验证出了macro和micro两种F1-score的计算方法。

请看下面的简单例子：

让$N=3,L=3$，一共有3个data，每个data有3个预备分类。

y_gt = np.array([[1,0,1],[0,1,1],[0,1,0]])
y_pred = np.array([[0,0,1],[1,1,1],[1,1,1]])

print("Macro f1-score:",f1_score(y_gt,y_pred,average='macro'))
print('Micro f1-score:',f1_score(y_gt,y_pred,average='micro'))

Macro f1-score: 0.6
Micro f1-score: 0.6666666666666666

对于每一个class，我们都需要先算一个2x2的confusion matrix，里面分别标明了对于这一个class的TP，FP，FN和TN。其实做法和多分类是一样的。

1. Macro-average方法

对于macro，我们通过每一个class的confusion matrix算出它的precision和recall，并计算出对与那个class的F1 score，最后通过平均所有class的F1 score得到F1 macro

Class 0：

gt\pred	1	0
1	0	1
0	2	0

$P_0 = \frac{0}{0+2}=0, R_0 = \frac{0}{0+1}=0$

$F1_0=\frac{2\times0\times0}{0+0}=0$

Class 1：

gt\pred	1	0
1	2	0
0	0	1

$P_1 = \frac{2}{2+0}=1, R_1 = \frac{2}{2+0}=1$

$F1_1=\frac{2\times1\times1}{1+1}=1$

Class 2:

gt\pred	1	0
1	2	0
0	1	0

$P_2 = \frac{2}{2+1}=\frac{2}{3}, R_2 = \frac{2}{2+0}=1$

$F1_2=\frac{2\times{\frac{2}{3}}\times1}{\frac{2}{3}+1}=\frac{4}{5}$

$F1_{macro}=\frac{1}{N}(F1_0+ F1_1+…+F1_N)=\frac{1}{3}(F1_0+F1_1+F1_2)=\frac{1}{3}(0+1+\frac{4}{5})=0.6$

2. Micro-average方法

对于micro，我们把所有class的binary confusion matrix整合成一个大的2x2confusion matrix，然后并对于整合成的confusion matrix算出一个precision和recall值（$P_{comb}$ and $R_{comb}$），最后通过公式得到$F1_{micro}$ score。

Combined all classes: