Alleviating the Inconsistency Problem of Applying Graph Neural Netwrok to Fraud Detection

GNN

发布日期: 2020-12-15

GraphConsis模型建立在异质信息网络之上，考虑反欺诈工作中的inconsistency问题，对GNN的Aggregation函数进行改进，综合了GraphSAGE的采样思想和GAT的注意力权重思想，将它们运用到异质信息网络中。

是一种Supervised的方法。需要区别Semi-supervised和transductive的区别！：Semi-supervised的损失函数包括supervised loss和unsupervised loss两个的结合，而transductive的损失函数只包含supervised loss！

文章信息：

@inproceedings{liu2020alleviating,
  title={Alleviating the Inconsistency Problem of Applying Graph Neural Network to Fraud Detection},
  author={Liu, Zhiwei and Dou, Yingtong and Yu, Philip S. and Deng, Yutong and Peng, Hao},
  booktitle={Proceedings of the 43nd International ACM SIGIR Conference on Research and Development in Information Retrieval},
  year={2020}
}

1. Background 背景知识

随着GNN的流行，其被广泛地运用到欺诈检测领域。基于GNN的欺诈检测优点是在结合原有的Feature的基础上，引入节点与节点之间的关系，从而更好地学习Node Embedding，提供一种End-to-End的Semi-Supervised的学习方式。

GNN的核心在于Neighborhood Aggregation，Neighborhood Aggregation基于的一个假设是邻居之间的feature和label应该是similar（或者说是consistent）。例如，正是因为这个假设，我们能够用GNN进行Community Detection。

然而，在欺诈检测中，这个假设被削弱了，欺诈者往往潜伏在良性用户之中，因此，如果不进一步对邻居进行筛选，而是直接聚合的话，在认知上是不正确的，欺诈用户会因此成功伪装自己。这就是本论文要讨论的inconsistency问题：

Context Inconsistency

如上图，聪明的欺诈者可以将自己与良性用户联系起来，$v_1$作为fraudster，它的邻居中包含了良性用户$v_4,v_6,v_7$，如果在邻居聚合过程中，聚合了它们的信息，无疑会使得欺诈检测的难度变大。

因此，要想办法在聚合的时候，筛去这些context inconsistency的邻居。

Feature Inconsistency

举一个例子，假设现在进行review fraud detection，一个user发表了两条review，因此我们将两条review之间连一条边（因为它们来自同一用户），两条review因此成了邻居，然而它们的内容可能天差地别，如果在邻居聚合过程中，聚合了它们的信息，无疑会使得欺诈检测的难度变大。

例如，上图中$v_1$与$v_4,v_6,v_7$。（这个例子不太好，即使都是良性也有可能Feature Inconsistency的）

Relation Inconsistency

如上图，在Relation Ⅱ下，fraudster更易与fraudster相连，这说明，Relation Ⅱ对欺诈检测来说贡献更高，我们更希望聚合来自Relation Ⅱ的邻居信息。

2. Contributions 贡献

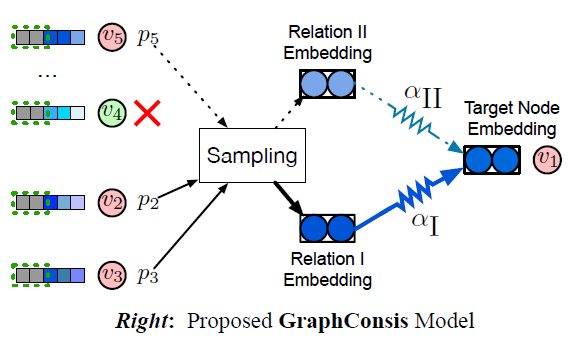
为了解决3个inconsistency的问题，论文提出GraphConsis模型，对应的解决办法如下：

context inconsistency：to handle the context inconsistency of neighbors, GraphConsis assigns each node a trainable context embedding, which is illustrated as the gray block aside nodes in Figure（Right）
feature inconsistency：Secondly, to aggregate consistent neighbor embeddings, we design a new metric to measure the embedding consistency between nodes. By incorporating the embedding consistency score into the aggregation process, we ignore the neighbors with a low consistency score （e.g. the node v4 is dropped in Figure （Right）） and generate the sampling probability.
relation inconsistency：Last but not least, we learn relation attention weights associated with
neighbors in order to alleviate the relation inconsistency problem.

本论文的贡献：

第一个提出GNN based fraud detection中存在inconsistency问题，并且提出解决办法的；
通过实验验证了3种inconsistency问题对GNN based fraud detection的结果影响；（见@4. 实验）
提出GraphConsis模型，模型通过context embedding，neighborhood sampling，relational attention三种方法，解决了3种inconsistency问题。

3. Model：GraphConsis⭐

Model Illustration

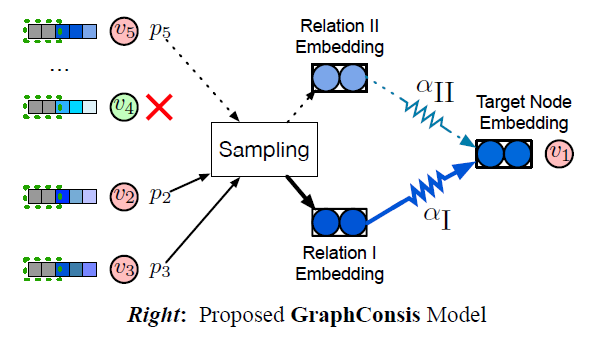
Context Embedding

为了解决context inconsistency的问题，在模型的第一层，引入一个trainable context embedding ${\bf {c}}_v$ for every node：

$$
{\bf {h_v}}^{(1)} = \lbrace {\bf {x_v}} || {\bf {c_v}} \rbrace \oplus AGG^{(1)}(\lbrace {\bf {x_{v’}}} || {\bf {c_{v’}}} : v \in {\mathcal {N_v}} \rbrace)
$$

论文中说，这个context embedding能够代表节点的local structure，至于为什么代表我就不清楚了。而且怎么对于未知的样本生成 ${\bf {c}}_v$也是一个问题。

Neighbor Sampling

为了能够聚合更加相关的邻居，首先定义了邻居之间的consistency score：

$$
s^{(l)} (u,v)= \exp (-|| {\bf {h_{u}}}^{(l)} -{\bf {h_{v}}}^{(l)} ||_{2}^{2})
$$

然后设定一个阈值$\epsilon$，筛选掉那么consistency score低于$\epsilon$的邻居。

对于剩下来的邻居$\tilde {\mathcal {N}} _v$，根据它们的consistency score计算它们被采样的概率：

$$
p^{(l)} {(u;v)} = s^{(l)} {(u,v)} / \sum_{u \in \tilde {\mathcal {N}} _v} s^{(l)} {(u,v)}
$$

每一层都有重新计算采样概率。

Relation Attention

我们使用一个向量${\bf {t}} _r$表示关系类型$r$，然后使用这个向量得到每个neighbor的注意力分数：

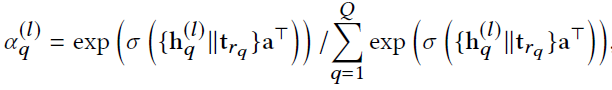
其中$r_q$表示第$q$个采样样本连接到当前节点的relation类型。

得到注意力分数之后就可以直接进行“加权”聚合了：

因此，Relation Attention是寄托在邻居的消息聚合之上的，并不是独立的。

4. Experiments 实验

数据集

数据集名称：YelpChi spam review dataset
这个数据集包含Yelp上酒店和餐厅的评论

预处理数据集包括：

29431 users
182 products
45954 reviews

构图⭐

review作为图中的node，根据下面三种关系构建node之间的边：

R-U-R：两条review来自同一个user；
R-S-R：两条review来自同一product下的同一rating；
R-T-R：两条review来自同一product下的同一月份;

node（即review）的初始特征$\bf x$是使用Word2Vec提取出来的100维的vector。

任务

a spam review classification，一个二分类问题。

Benchmark

Cora
PPI
Reddit

Baseline

Logistic Regression
FdGars
GraphSAGE
Player2Vec

度量指标

F1-score
AUC

The Inconsistency Problem

下面是关于Benchmark和YelpChi数据集的统计信息，除了统计Nodes和Edges，我们还统计了$\gamma^{(f)}$和$\gamma^{(c)}$。

context characteristic score

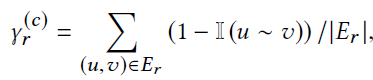
feature characteristic score

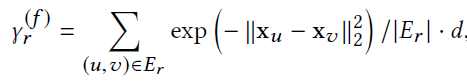
Benckmark（Cora，PPI，Reddit）数据集并不是反欺诈数据，所以它们很难体现我们之前说的3种Inconsistency问题。

使用上面的两个指标，我们可以来讨论在真实的反欺诈研究中，数据集体现的Inconsistency问题：

Context Inconsistency：如Table 1所见，除了R-U-R关系集，其他的三个真实数据集都体现了极低的$\gamma^{(c)}$；
Feature Inconsistency：观察$\gamma^{(f)}$，发现结果都挺高的；
Relation Inconsistency：还是如Table 1所示，不同的Relation导致了不同的$\gamma^{(c)}$和$\gamma^{(f)}$；

Performance Evaluation

结果分析：

GraphConsis在训练样本为60%和80%的时候，才能体现更优秀的结果；
一个更有趣的现象是，传统的LR居然比GNN的性能更好😨为什么捏？

可能正是因为存在着Inconsistency的问题，导致这些GNN方法在Aggregation的过程中聚合了很多无用的信息；
Player2Vec，FdGars和GraphSAGE的结果表明，GraphConsis的neighbor sampling和relation attention的作用。

我的思考

可以结合SemiGNN和GraphConsis

考虑到在SemiGNN的feature work中有提到要考虑不同的relation信息，因此可以引入GraphConsis的思想。关于relation的影响，也可以继续从GNN based HIN中进行探索。
GraphConsis中提到了自己的feature work

Future work includes devising an adaptive sampling threshold for each relation to maximize the receptive field of GNNs.（这个可以考虑GeniePath，使用循环神经网络来构造感受野）
Investigating the inconsistency problems under other fraud datasets is another avenue of future research.（比如我的任务——金融反欺诈）

CarlYoung

http://yc1999.github.io/2020/12/15/alleviating-the-inconsistency-problem-of-applying-graph-neural-netwrok-to-fraud-detection/