[TOC]
Sequence Labeling
序列标注问题,输入一个Sequence,对应在其每个position输出一个class。

如上,RNN可以做这个问题。但是我们今天的方法与 RNN 有差别,具体差别将在下面讲述。
POS tagging
今天以 POS tagging 为例,在英文上,这个问题甚至算是一个已经被解决的问题。
Outline
- Hidden Markov Model (HMM)
- Conditional Random Field (CRF)
- Structured Perceptron / SVM
- Towards Deep Learning
Hidden Markov Model (HMM)

我们人类怎么产生一个句子呢?首先,在心中产生一个文法,接着匹配单词。这是 HMM 的假设。
我们假设,我们脑中的文法,是马尔可夫链(Markov Chain)构成的。我们的某个文法,有自己出现的概率。这是第一步。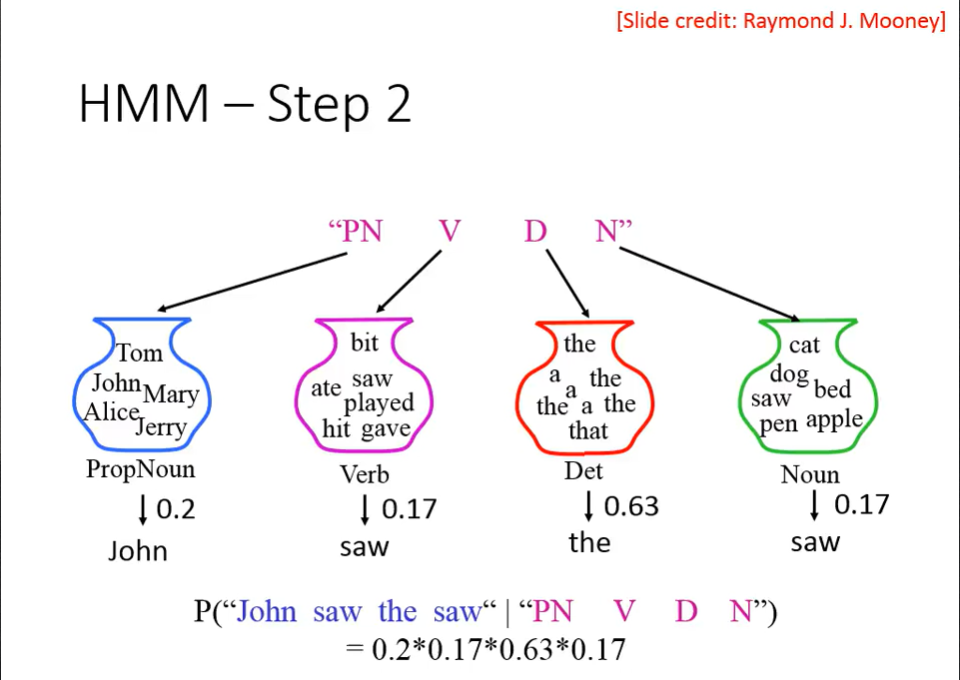
接着,第二步,我们衡量各个单词在词义上的出现概率。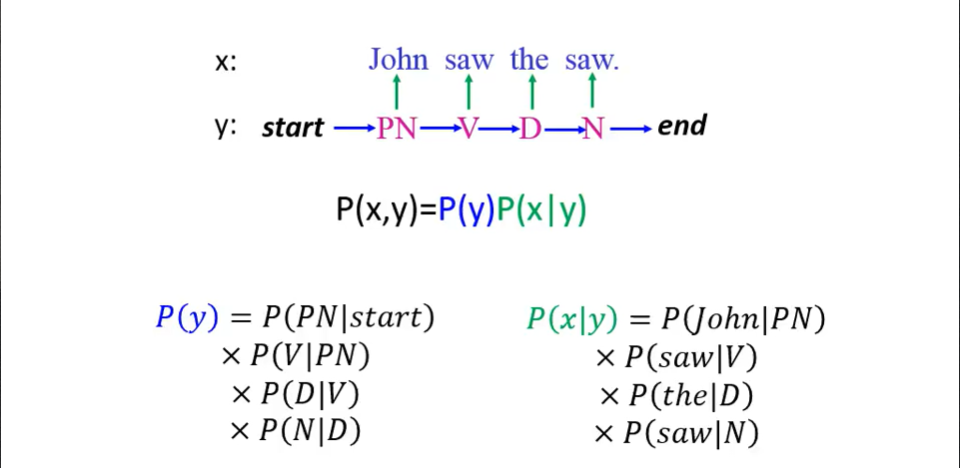
最终,我们由条件概率公式,得到$P(x,y)$。
总结一下,第一步是计算 Transition probability ,第二步是计算 Emission probability 。
Estimating the probabilities

HMM是基于计数的,依赖于我们的training data。我们由训练数据得到各个概率。
How to do POS Tagging?

如上, x 是给定的,我们找出最可能的 y 即可。上面也说明了Hidden Markov Model名字的由来。
但是,我们找 y 的过程,需要穷举 y 吗?可以使用 Viterbi Algorithm 。
Drawbacks

HMM 存在哪些问题呢?如上,尽管我们通过数据训练得到了两种 probability 的数据,并且也得出$y_1$最有可能是$V$的结论。
但是,$N: D: a$这个序列其实是实实在在出现过的数据,而我们实际使用时,遇到了$N: : a$却无法把$D$填在其中。
因此,HMM 会“脑补”一些序列。这件事有好有坏:
- 可以弥补 training data 的不足;
- 但是容易出现如上的问题。
或许我们可以建立更复杂的模型弥补缺点;但是,我们还可以使用 CRF ,并且不用建立更复杂的模型。
Conditional Random Field (CRF)

其假设,$P(x,y)$与$exp(w \cdot \phi(x,y))$成正比。可以做出变换如上。
其实,CRF 与 HMM 的区别并不大。
上述 $P(x) = \sum_{y’}P(x,y’)$ 使用的是全概率公式计算的。
P(x, y) for CRF

在 HMM 中,对 P(x, y) 取 log 。
如上,把最后一项做一个转换。为什么可以做这个转换呢?我们下面举一个直观的例子。
如上,李老师举了一个很直观的例子(其实最后,前面的求和符号应该去掉)。
我们对所有的项都做这个转换。
这样我们就相当于对两个向量求了内积。这样,HMM 与 CRF 其实就是一回事了。
可以说,HMM是CRF的一种特殊的情况,CRF的w并不做任何限制,是一个需要通过训练得到的vector,而HMM是限制w的取值之后得到的结果。
如上,我们在训练时,w是可正可负的,如果 w 是大于 0 的话,那由$P = e^w$转换,得到的$P$大于 1 ,则很奇怪。
因此,我们在 CRF 中,不做等号,而作“正比”关系。
Feature Vector——$\phi(x,y)$

如上,特征向量可分为两部分:
- 第一部分,是 tag 与 word 间的关系,并且维度是二者维度的乘积;

- 第二部分,是 tag 与 tag 之间的关系,要注意,要带上 Start 与 End 的向量。
- 此外,你还可以在 CRF 中自己定义Feature Vector。
Training Criterion

有些像交叉熵,最大化我们见过的序列对,最小化我们没见过的序列对。
使用梯度上升即可。
Training

经过一些运算,得到一个具有物理含义的微分式子:
- 出现次数越多,对应地 w 越大;
- 如果 s 与 t 出现在任意其他对中出现的次数也很大,那则应该把 w 减小。
- 二者有 trade-off ;
- 无需穷举$y’$ ,可以用 Viterbi Algorithm 来求解。

有特征向量定义,得到最终更新式如上。
CRF v.s. HMM

如上,HMM 并不减少没出现过的项的几率。还是之前的例子,CRF 更倾向于通过历史数据调整概率值。
Synthetic Data

如上,是一个对比 CRF 与 HMM 的实验。
如上,横纵轴代表 HMM 与 CRF 犯错的百分比。当 α < 1 2 \alpha < \frac{1}{2}α<21 时,CRF 的结果更好。
Structured Perceptron / SVM
Structured Perceptron

其在本文题的建模如上。
Structured Perceptron v.s. CRF

如上,Structured Perceptron 其实与 CRF 的更新式很像。
Structured SVM

如上,Structured SVM 中的特别之处就是,要考虑 error 这件事情。
如上,我们不再是找 a r g max y [ w ⋅ ϕ ( x n , y ) ] arg \max_y [w\cdot \phi(x^n,y)]argmaxy[w⋅ϕ(x**n,y)] ,而是带上了 Δ ( y ^ n , y ) \Delta (\hat{y}^n,y)Δ(y^n,y) 。如果我们使用如上方式建模,定义 Δ ( y ^ n , y ) \Delta (\hat{y}^n,y)Δ(y^n,y) ,可以求解,否则,不一定能求解。
Performance of Different Approaches

如上,Structured SVM 是表现最好的。
How about RNN?

如上,RNN的缺点是,没有考虑整个序列。但是双向的 RNN 可能会弥补这个缺点。
此外,我们可以把 label 的关系考虑进去,比如一定不考虑“声母接声母”。
但是,RNN 可以 Deep ,因此最终是 RNN 最强。
Integrated together⭐
我们可以将二者结合。
如上,我们用深度神经网络来计算 $P(x|y)$ ,再赋给结构化学习。我们做了一个小小的改变: $P(x|y) = \frac {P(y|x)P(x)} {P(y)}$,并且不管$P(x)$。

此外,在 Semantic Tagging 中,二者结合也十分常见。
Concluding Remarks




